Chapter 1: Understanding Euler's Formula

Euler’s formula, often regarded as one of the most stunning equations in mathematics, is represented as e^(i*pi) + 1 = 0. This elegant expression encapsulates several vital mathematical ideas and extends its influence into various domains, including physics and artificial intelligence.

In machine learning, Euler's formula plays a pivotal role in the representation and handling of intricate data. For instance, it allows the representation of high-dimensional data as complex numbers, facilitating easier analysis and manipulation. This is especially beneficial in unsupervised learning, where it aids in reducing data dimensionality. Additionally, in neural networks, Euler’s formula is utilized to model dynamic network behavior and enhance overall performance.

In the realm of natural language processing, this formula is instrumental in analyzing text data. For example, it helps in sentiment analysis by representing text as complex functions, allowing transformations such as rotation, scaling, and translation to uncover the intent, emotion, and context behind the text.

Euler’s formula also finds applications in computer vision, where it can represent images as complex functions to assist in tasks like image recognition and object detection.

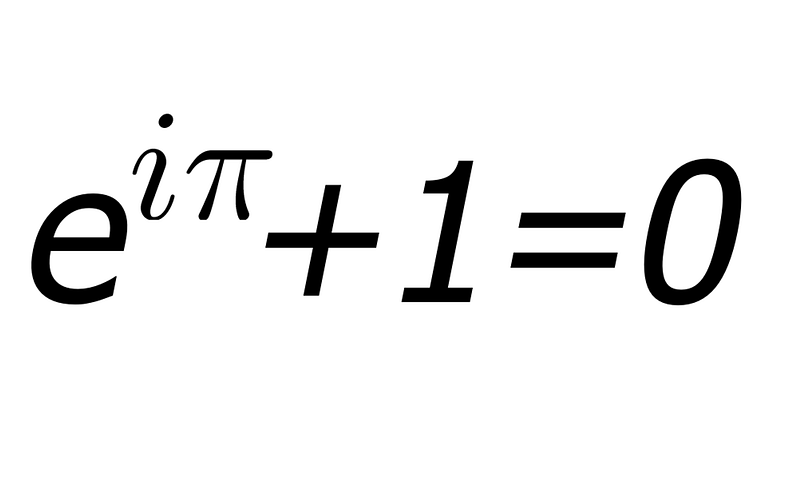
Chapter 2: The Legacy of Euler

This equation is named after Leonhard Euler, an 18th-century Swiss mathematician. Euler's prolific contributions to various mathematical fields, such as calculus, trigonometry, and number theory, are profound. His formula connects five fundamental mathematical constants: e (the base of natural logarithms), i (the imaginary unit), π (the ratio of a circle's circumference to its diameter), 0 (the additive identity), and 1 (the multiplicative identity).

At the heart of Euler's formula lies the concept of complex numbers, which can be expressed as a + bi, where a and b are real numbers and i represents the imaginary unit (the square root of -1). The formula states that for any real number t, e^(it) = cos(t) + i*sin(t), illustrating a relationship between complex numbers and trigonometric functions.

In mathematics, Euler’s formula aids in simplifying complex integrals and solving differential equations. In physics, it is vital for wave mechanics, appearing in solutions to the Schrödinger equation that describes quantum systems. The formula also emerges in studies related to electricity and magnetism.

Euler's formula is sometimes referred to as "God's Equation" because it symbolizes the universe's underlying unity and order, merging concepts from algebra, trigonometry, calculus, and the complex plane, often linked to infinity.

Despite its profound implications, the beauty of Euler’s formula lies in its simplicity. It encapsulates a vast array of mathematical ideas in a straightforward equation, making it accessible even to those unfamiliar with complex number theory or calculus. This clarity is why it frequently serves as a foundational concept when introducing complex numbers and exponential functions to students.

Moreover, Euler's formula connects to numerous other mathematical disciplines, including group theory, number theory, and topology. In group theory, it defines the unitary operator, which describes physical system symmetries. In number theory, it aids in calculating distinct solutions to specific equations known as Diophantine equations. In topology, the equation relates to the winding number of closed curves in the complex plane.

Another fascinating aspect of Euler's work is its historical context; he was not the first to express this formula, yet he was the first to publish it in its current form in 1748. Previous mathematicians, like De Moivre, had utilized similar expressions linking trigonometric functions to complex exponentials, but Euler's presentation solidified the relationship.

Chapter 3: Applications of Euler's Formula

In signal processing, Euler’s formula helps represent and manipulate time-varying signals. For instance, sinusoidal signals can be expressed as complex exponentials, simplifying their analysis. In control systems, it aids engineers in designing systems that accurately follow desired trajectories.

In telecommunications, Euler’s formula is vital for representing signal modulation and evaluating communication system performance. It is particularly useful in designing wireless communication systems, modeling signal propagation through the atmosphere, and optimizing overall system performance.

Beyond these fields, Euler’s formula is also significant in image and video processing. It enables the analysis and manipulation of images as complex functions, allowing for transformations like rotation and scaling. In video processing, it represents sequences of images, facilitating efficient storage and transmission through techniques like video compression.

In the domain of artificial intelligence, Euler’s formula is essential for representing and manipulating complex data in machine learning, enhancing the efficiency of data analysis and neural network performance.

Chapter 4: Other Elegant Equations in Mathematics and Physics

Many other remarkable equations exist in mathematics and physics, each illuminating different aspects of the natural world and the universe's structure. Notable examples include:

• Pythagorean Theorem: a² + b² = c², illustrating the relationship among the sides of a right triangle, with extensive applications in various fields.
• Gaussian Distribution: This equation describes the probability distribution of numerous naturally occurring phenomena and is widely used in statistics.
• Schrödinger Equation: Fundamental to quantum mechanics, it describes the temporal evolution of a quantum system's wave function.
• Navier-Stokes Equations: These equations govern fluid motion and are foundational in computational fluid dynamics simulations.
• Wave Equation: Describing wave behavior in various mediums, it is crucial in the study of sound, light, and water waves.
• Euler-Lagrange Equation: Used in physics to determine the path of a system that minimizes energy.

Each of these equations represents a unique aspect of the natural world, contributing to our comprehension of the universe's workings.

Chapter 5: Recommended Reading on Beautiful Equations

To delve deeper into the beauty of equations in mathematics and physics, consider these titles:

• "The Beauty of Fractals" by Heinz-Otto Peitgen and Peter Richter explores the captivating world of fractals, showcasing stunning visuals and underlying mathematical concepts.
• "The Elegant Universe" by Brian Greene offers insights into string theory, providing a detailed yet accessible explanation of its implications for our understanding of the cosmos.
• "Einstein’s Equations" by Oliver Knill introduces the mathematics of general relativity and its applications.
• "The Equations of Life" by Charles S. Cockell examines the equations crucial for understanding life’s origin and evolution.
• "The Art of Equation" by Ian Stewart explores the significance of various equations in daily life.
• "Beautiful Minds" by Brian Hare and Vanessa Woods investigates behavioral equations and cognition in great apes and dolphins.

Chapter 6: Leonhard Euler: A Brief Biography

Leonhard Euler (1707–1783) was a Swiss mathematician and physicist who made significant contributions across multiple fields, including calculus, trigonometry, and number theory. Recognized as one of history's greatest mathematicians, his work remains influential in various scientific domains.

Born in Basel, Switzerland, Euler began his mathematical journey early and studied at the University of Basel under Johann Bernoulli. He later joined the St. Petersburg Academy of Sciences in Russia, where he spent over 25 years making groundbreaking contributions.

Despite losing his eyesight in 1741, Euler produced an extraordinary volume of work, including over 800 papers and books. His "Letters to a German Princess" popularized mathematics and illustrated its everyday applications.

Euler passed away in 1783, leaving behind a legacy of profound mathematical concepts and formulas named in his honor, such as Euler’s formula and Euler’s number.

In conclusion, Euler's formula stands as a testament to the beauty of mathematics, uniting seemingly disparate concepts—exponential functions, trigonometry, and complex numbers—into a single, elegant equation. Its simplicity, historical significance, and broad applicability cement its status as a true masterpiece in the realm of mathematics.

Chapter 7: Visual and Video Insights

This video, titled "The God Equation: Euler's Identity," delves into the profound implications of Euler's formula in mathematics and beyond.

In this video, "Physics' Greatest Mystery: Michio Kaku Explains the God Equation," renowned physicist Michio Kaku explores the significance of Euler's identity and its connection to the universe.