The Law of Large Numbers

This gambling method seems to be reinforced by the Law of Large Numbers. Let's denote N as the total number of betting rounds, and n? | n? as the frequency of odd or even results appearing on the die. According to the Law of Large Numbers, when N is sufficiently high:

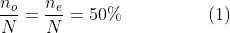
Equation (1) indicates that the frequency of odd numbers should closely match that of even numbers over a large number of rolls. Consequently, if the die has shown even numbers for the past ten rounds, it seems highly probable that an odd number will appear next… or does it?

The flaw in this reasoning lies in the fact that for Equation (1) to hold true, N must be significantly larger than 10. A general guideline suggests that N should be at least 50. The financial implications for everyday gamblers are considerable. If a player starts with a $1 bet and continues to double it after each loss, they will need to wager $2, $4, $8, and so on, leading to an exponential increase that reaches $1,024 after ten rounds, totaling $2,046. What if the player began with a $10 or $20 bet due to minimum wagering requirements at most casinos?

Moreover, within a sufficiently large N, there can be streaks of odd numbers appearing before being countered by even numbers, all while still complying with the Law of Large Numbers.

From another angle, consider that the casino itself acts as a 'gambler' applying the same strategy (betting against players who double their bets), but with significantly more capital. Thus, although initiated by the gambler, this strategy ultimately favors the casino.

The Roulette Factor

Casinos employ additional mechanisms to their advantage. For instance, many casino games are inherently skewed against players. In the previous example, we assumed a fair die. However, in reality, dice games often use multiple dice (e.g., three dice), and if all dice show the same number, all players lose their bets. Therefore, Equation (1) will invariably yield a result below 50%.

This bias is even more pronounced in games like Roulette. In most casinos, players select a number between 0 and 36 (which totals 37 possible outcomes), and if their chosen number wins, the payout is only 35 times the wager. This means that players do not receive a fair return relative to the risks they take, allowing casinos to retain the difference.

For further insights, you can explore the game guide for Roulette at a casino in Sydney, Australia, which has recently faced scrutiny for alleged money laundering practices. Ultimately, casino games are designed to ensure profitability for the house.