Exploring the Double-Slit Experiment: A New Perspective
Written on
Chapter 1: Unraveling the Double-Slit Mystery
In 1801, Thomas Young made a groundbreaking discovery when he demonstrated that shining light through two slits simultaneously creates an interference pattern on a wall behind the slits, akin to the behavior of water waves. This pivotal finding laid the groundwork for his wave theory of light, yet he could not have anticipated the profound complexities that would emerge from similar experiments over two centuries later.
Fast forward to 1927, when Davisson and Germer conducted a double-slit experiment using individual electrons rather than a continuous light beam. As each electron passed through the slits, it would strike a crystalline nickel target, leaving behind a tiny dot. Initially, one might expect to see two clusters of dots—one for each slit—akin to classical particle behavior. However, the dots instead gradually formed a wave interference pattern, much like Young's original experiment. This indicated that the electrons, despite being fired one at a time, were somehow interfering with themselves as waves while impacting the wall like discrete particles. This peculiar behavior was also noted with larger entities, such as atoms and even molecules.
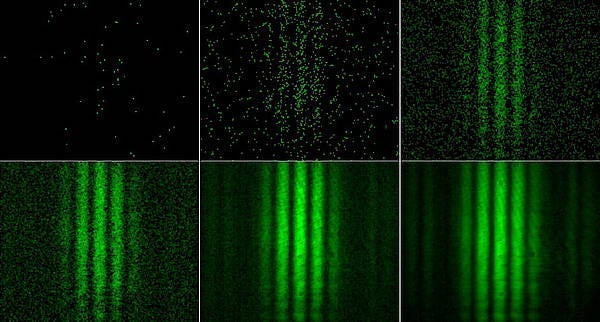
Wave interference pattern, particle by particle
Subsequent research revealed another astonishing aspect: introducing a particle detector at one of the slits to determine which one the particle passed through resulted in the disappearance of the wave interference pattern. Instead of forming a continuous wave pattern, the impacts produced two distinct clusters, similar to what would be expected from classical particles. The underlying reason for this phenomenon remains elusive.
Section 1.1: The Copenhagen Interpretation
The Copenhagen Interpretation of quantum mechanics posits that, on a quantum scale, reality is indeterminate. Before measurement, particles lack definite locations. Instead, a wave function described by the Schrödinger equation outlines the probabilities of where a particle might be detected. Until measurement occurs, the particle exists in a superposition of possible positions, collapsing to a single location upon observation.
This "probability wave" is not simply theoretical; it represents the real source of the observed distribution of particle impacts. Despite the mathematical framework of quantum theory being widely accepted for explaining atomic and subatomic phenomena, physicists have struggled to find consensus on the metaphysical implications of its most profound mysteries. Some embrace the idea of indeterminism, while others resist it.
To illustrate this, consider a roulette wheel. One can model the possible outcomes of a spin using probabilistic mathematics. Yet, it is inaccurate to assert that these probabilities influence the physical wheel. Outside quantum mechanics, deterministic laws generally underlie probabilistic results. In the quantum realm, some physicists contend that fundamental laws operate on an indeterministic basis, with particle positions defined by probability equations.
The only explanation that has significantly alleviated the philosophical dilemmas surrounding the probability wave is Hugh Everett III's relative-state theory, originally termed the "Theory of the Universal Wave Function," and now commonly referred to as the "Many-Worlds Interpretation."

Section 1.2: Hugh Everett's Many-Worlds Interpretation
Everett's theory posits that all existence is part of a universal wave function, eliminating the need for wave-function collapse. In parallel universes, every potential particle location foreseen by the wave function manifests as a distinct branch of reality. To any given observer, a particle appears at a single position, while other branches of the same particle exist at different locations relative to other observers, who remain unaware that they are merely one among countless nearly identical copies. Our observations do not collapse the wave function; they simply reveal our position within a specific momentary branch of the universal wave function.
This framework is enticing as it maintains a mechanical determinism, yet remains subjectively probabilistic. There is no requirement for an arbitrary wave collapse. Indeterminism, rather than being a fundamental characteristic of the universe, stems from the subjective experiences of observers, whose seemingly linear existence traverses a vast array of branching pathways.
Despite the growing popularity of Everett's Many-Worlds Interpretation, it is not without its detractors. The concept may sound far-fetched, reminiscent of science fiction. It represents our best attempt at a metaphysical explanation for the double-slit experiment but relies heavily on an incomplete and unverifiable logical abstraction that conflicts with our established understanding of space and time.
The pressing questions remain: Where are these parallel universes, and how do they fit within the four-dimensional framework proposed by General Relativity? Moreover, how does the wave interference pattern manifest between these parallel universes, and why does it vanish when we measure the energy passing through the slits? If we could find answers to these queries, it would strengthen the case for Everett's theory and potentially resolve ongoing debates.
Chapter 2: Visualizing the Fourth Dimension
According to General Relativity, our reality is four-dimensional, comprising three spatial dimensions and one temporal dimension. In a forthcoming article, I will argue that reality is indeed four-dimensional, but that time should be considered dimensionless, with the four dimensions being entirely spatial. For now, I aim to convince you of the existence of this fourth dimension, which is more accessible to conceptualization than it may initially seem.
The question of parallel universes presents a significant barrier to the acceptance of the Many-Worlds Interpretation. We are asked to believe in something invisible and difficult to visualize. Many tend to picture a parallel universe as something extremely distant, as if our universe is a giant bubble with other similar bubbles existing just outside it ad infinitum. Popular culture often depicts Everett's theory in this manner:

These illustrations are fundamentally flawed. If a fourth dimension exists, then "parallel universes" need not be unimaginably far apart; they could be stacked directly on top of one another, with the x, y, z coordinates of one branch nearly coinciding with those of another.
To properly conceive our relationship with a fourth dimension, we can scale down our perspective and consider how a two-dimensional reality relates to a third dimension.

Imagine this playing card as a two-dimensional universe. If we rotate it slightly into the third dimension along the x-axis…

…we can visualize two identical universes in direct contact, nearly superimposed upon each other. By stacking multiple cards in this manner, we illustrate how they can be closely packed together, with one card almost perfectly overlapping the next. The crucial point is that they are all touching, occupying the same x and y space yet remaining invisible to one another due to slight translations in the third dimension.
In the preceding image, I chose to rotate around the x-axis, which means that each x coordinate remains constant across the parallel universes, while the y and z coordinates change incrementally with the rotation. Similar reasoning could apply if we rotated around the y-axis, altering the x coordinates incrementally with z.
By introducing a fourth dimension into our three-dimensional reality, we have three distinct ways to rotate the space into this higher dimension. Let’s refer to this dimension as the imaginary dimension and represent it with imaginary numbers, similar to my previous discussion on Euler’s Formula. By adjusting x, y, or z slightly into the i dimension, we create a parallel space that is in direct contact with the original, sharing two of its original Cartesian coordinates while being infinitesimally displaced in the third.
Consequently, our nearest parallel selves may not be far away at all; they exist superimposed upon us, inhabiting the same three-dimensional space. The "parallel universes"—noted in quotes because from a broader perspective, they represent the same universe—are slightly out of sync with us in the fourth dimension, yet overlap with our reality.
With this continuous superposition, it becomes easier to grasp how one universe can interfere with another at the quantum level. Nonetheless, we still need to clarify the outcomes of the double-slit experiment. How does the wave interference pattern emerge particle by particle? And why does it vanish when we ascertain which slit a particle traverses?
The answer to the first question becomes evident through our exploration of the fourth dimension. When we assert that a point particle interferes with itself, we do not convey the full picture. The particle represents merely a fragment of a wave that extends continuously across a rotation in the fourth dimension or, alternatively, across numerous parallel branches that are either in direct contact or situated extremely close to one another. The interference occurs not between the "particle itself," but rather between the particle and the infinite copies of itself that are closely superimposed.

When we launch this “individual particle” at the double-slit and the wall behind it, we are effectively sending a four-dimensional wave.
In the following illustration, we depict the double-slit experiment, with many particle trajectories culminating in a wave interference pattern after numerous trials. However, we could just as easily interpret this image as a representation of a single trial, a single particle launch, viewed from the fourth dimension. From our limited three-dimensional perspective, we perceive only one of the impact points, yet all of them exist in nearby branches of space-time.

Now, let’s tackle the more challenging question: Why does the wave interference pattern disappear when we introduce a particle detector at one of the slits?
The straightforward answer is divergence. Engaging the particle detector does not "collapse" the wave function; rather, it complicates it. This interaction creates two distinct branches of reality: one where the detector is triggered and one where it is not. Every version of the particle passing through the right slit will continue to interfere among themselves, as will those passing through the left slit. However, the two groups have been separated by the detector's interaction, no longer existing in the near-perfect superposition necessary to produce a visible interference pattern. When we observe the point of light from the particle's impact, it remains part of a larger wave and wave interference pattern, but this interference now occurs only among the versions of the particle that traversed the same path and remain in the same relative state or branch of reality.
To illustrate, here’s a single test (one particle launch) without detectors:

All possible trajectories of the particles continuously interfere with one another, from one end to the other, until the wave impacts the wall, revealing one result from many.
With a detector in play, the two paths diverge due to the detection process. Reality bifurcates:

Repeating this test several hundred times yields clusters on the right and left. This outcome cannot be achieved without the bifurcation of the two sets. While a physical interaction with the detector might cause one set to become out of phase with the other and alter the interference pattern, it would not entirely eliminate the interference.
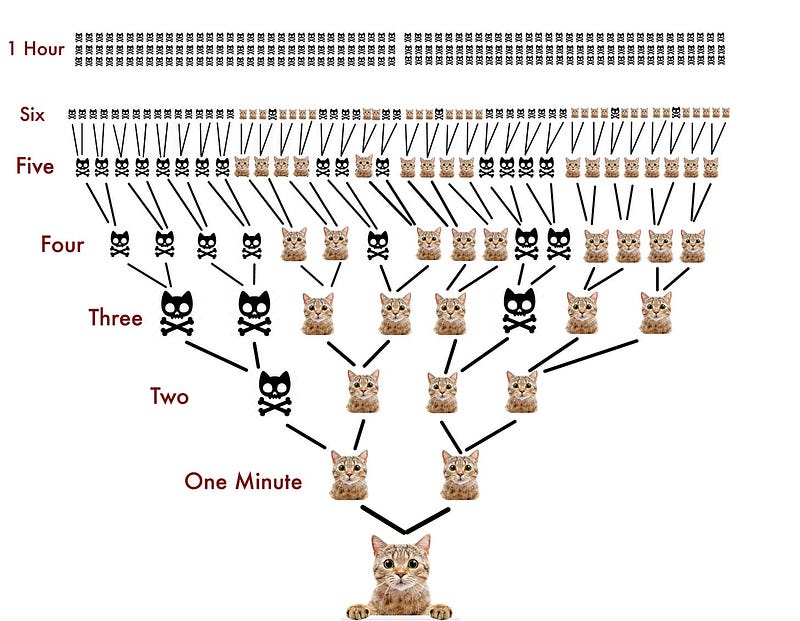
Next, what does this imply for Schrödinger's Cat? The renowned thought experiment entangles the macro state of a cat with the micro, quantum state of a particle's decay. Until we open the box, is the cat both alive and dead simultaneously?
We could argue that, yes, the cat occupies both states, but not within our own box. If I open the box after six minutes and discover the cat has been deceased for five minutes, I am located within a branch of time where it has unequivocally been dead for that duration. While there are branches of time where the cat is alive, those diverged from my timeline five minutes ago.
Albert Einstein famously dismissed the idea that God "plays dice with the universe." Edwin Schrödinger, who formulated the fundamental equation of quantum mechanics, similarly resisted the philosophical stance of his peers. He contended that there was nothing in the mathematics or his wave equation that indicated a collapse. He deemed it "patently absurd" that the wave function should be governed in two distinct manners: at times by the wave equation, and other times by the observer's direct interference, independent of the wave equation.
Everett's Many-Worlds Interpretation provides a framework that allows us to visualize a resolution to quantum mechanics, where the universe does not gamble with chance, but rather, we are the ones subjected to chance. Everything unfolds according to deterministic laws, yet our perspective remains subjectively indeterminate, akin to an infinite series of roulette spins, with each outcome hitting, and us only witnessing one result.
The lingering question pertains to the precise nature of reality's bifurcation. Does a local divergence imply that the entire universe diverges? When an electron in a remote galaxy faces a choice between two quantum paths, does this cause the entire Universe, including ourselves, to split? If so, to what degree is this splitting synchronous or asynchronous? Does time progress through discrete moments, each involving a bifurcation?
Only time will provide clarity.
The first video explores the intriguing concepts of quantum mechanics through the lens of the double-slit experiment, shedding light on its implications.
The second video offers a historical perspective on the original double-slit experiment, detailing its significance in the realm of physics.