Chapter 1: Introduction to Putnam

The Putnam competition is a prestigious mathematical contest, primarily held in North America, aimed at undergraduate students. It presents a series of challenging problems that test the limits of mathematical reasoning. Today, we will analyze one of these intriguing problems.

Section 1.1: Problem Overview

For this particular problem, known as Putnam 2008 B2, we begin by examining a few small values of n with a variable x. We find that F_0(x) is expressed as log(x), and F_1(x) is represented as x log x - x = x(log x - 1). To simplify our calculations, let’s compute the integral of x^n log x using integration by parts, which yields:

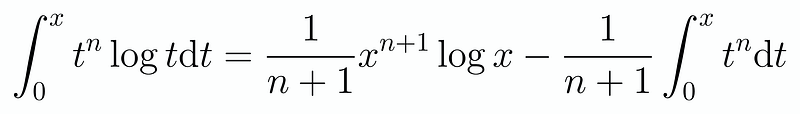
This results in the following:

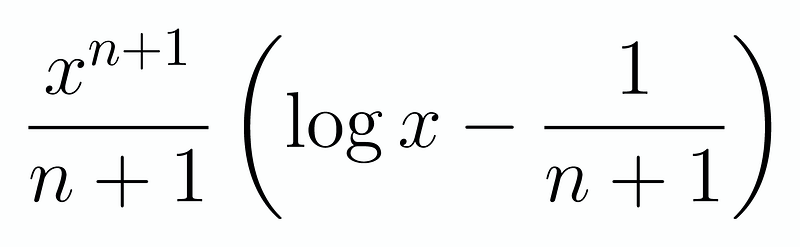
From our computations, we can infer a pattern. The logarithmic function remains constant, and the exponent of x consistently increases by one. Notably, the denominator appears to be multiplied by the subsequent integer. Thus, we can hypothesize the following form for F_n(x):

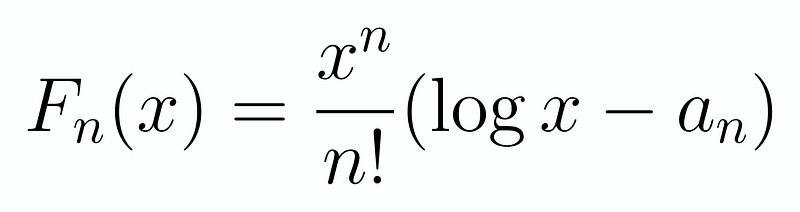
Section 1.2: Deriving a_n

Now, we need to determine the value of a_n while confirming that each F_n(x) adheres to the same structure. By integrating and applying the formula we derived, we find that F_(n+1)(x) can be expressed as:

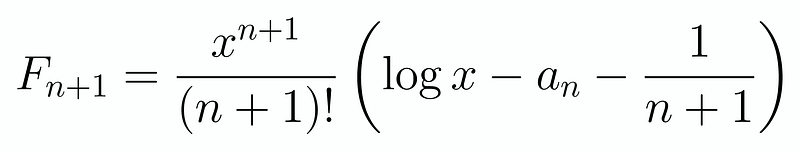
Consequently, we discover that a_n represents the sum of the first n reciprocals. With this knowledge, we can proceed to tackle the problem itself. Plugging this into our limit gives us:

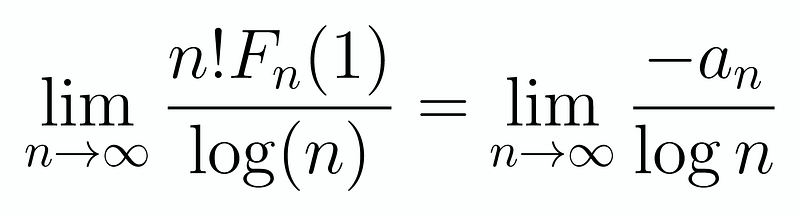
Given that log(1) equals 0, we now focus on evaluating this new limit. While it may be tempting to equate this to 0 due to the summation of constants over an infinite range, it’s crucial to remember the infinite nature of those constants.

Section 1.3: Establishing Bounds

To analyze a_n, we need to establish bounds. Notice that 1/x is a strictly decreasing function for positive x, allowing us to derive:

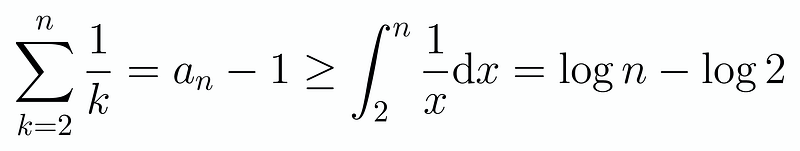
Next, we will explore an upper bound using a similar approach:

As n approaches infinity, the impact of these constants diminishes; thus, we can disregard them. Therefore, our limit simplifies to:

Ultimately, we arrive at our conclusion.

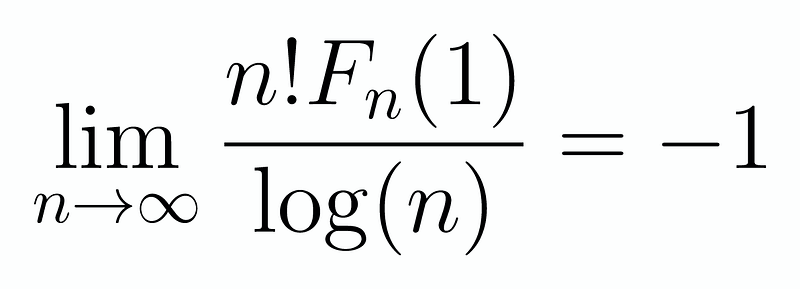
Exploring Additional Resources

For further insights into the techniques used in this problem, here are some recommended videos:

This video titled "Maximizing an Integral | Putnam 2006 B5" delves into integral maximization strategies that can enhance your understanding of similar problems.

Another useful resource is "Squeeze Theorem | Integration by Parts | Limits | Calculus | Putnam 2011 Problem A3," which covers foundational calculus concepts relevant to solving Putnam problems.

Enjoyed the content? If you found this helpful, consider supporting us! Your contributions make a difference!