Chapter 1: Introduction to the UK Integration Bee Finals

The UK Integration Bee finals took place last month in February 2024, presenting a plethora of intriguing problems. These range from straightforward to quite complex, yet most are immensely gratifying to tackle. Some problems feature notable cancellations, while others introduce clever techniques that may be new to many. In this article, we will delve into one such problem.

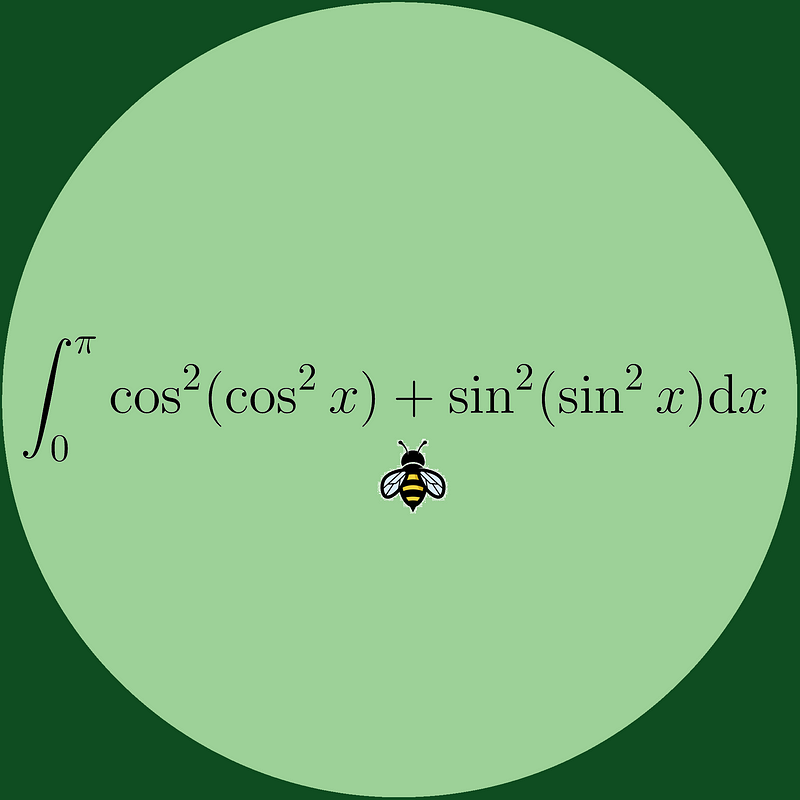
Chapter 2: Analyzing the Integral

This particular integral bears resemblance to the well-known identity cos²(x) + sin²(x) = 1. Our objective is to manipulate this integral into that recognizable form. We will begin by employing a common technique for solving trigonometric integrals: the substitution method, specifically using ( x ) as a variable. This approach is often referred to as the "king’s substitution."

Why is this technique advantageous? It allows us to keep the limits consistent while transforming the integral into a new form that may help simplify our calculations. Ideally, we hope to add this new integral back to itself, resulting in double the value of the original integral. Although our results may not always align perfectly with this expectation, in this case, we arrive at the same integral. This provides us a promising lead; we can safely halve the upper limit, indicating that we now possess half the value of our original integral. Thus, we can express our findings as follows:

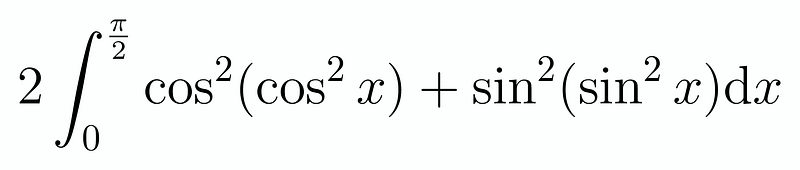
Chapter 3: Further Manipulation and Insights

Let’s apply our substitution technique again to explore further possibilities. We can express our integral as:

Upon reflection, we realize that if we combine these two expressions, we effectively double our original integral. This leads us to a remarkably elegant conclusion:

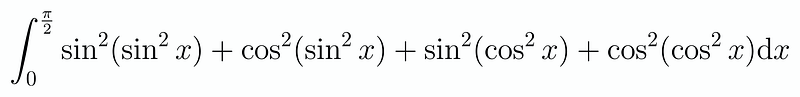
By pairing these terms and utilizing the identity sin²(x) + cos²(x) = 1, we can simplify our work even further:

This leads us to a concise conclusion: we find that our integral equals ( frac{pi}{2} ), and we have successfully completed the problem.

Chapter 4: Video Resources

For those interested in deeper exploration, check out these informative videos:

The first video, "MIT Integration Bee 2024 Finals Solutions," provides a thorough breakdown of the finals and the strategies used to tackle the problems presented.

The second video, "I tried a problem from the UK Integration Bee!" showcases a participant's personal experience and problem-solving approach at the UK Integration Bee.

If you appreciated this exploration, consider supporting us—it truly makes a difference!