Chapter 1: Introduction to Ninja Paths

The problem presented in the 2023 International Mathematical Olympiad (IMO) has garnered attention for its uniqueness and charm, particularly due to its ninja theme. It exemplifies an ideal IMO problem—accessible enough for capable high school students without requiring advanced university mathematics, yet still presenting a formidable challenge for the top contenders.

The score distribution for this problem reveals interesting insights. Less than 20% of participants earned the maximum score of 7 points, while 35% scored zero. For context, the students participating in the IMO are exceptionally talented in mathematics.

As we delve into the problem statement, it is relatively lengthy but becomes clearer when paired with the accompanying diagram. Let’s analyze it together.

Chapter 2: The Problem Statement

The core of the problem can be summarized as follows:

Let n represent a positive integer. A Japanese triangle is constructed with 1 + 2 + ... + n circles arranged in an equilateral triangle, where each row i contains exactly i circles, and one of these circles is colored red. A ninja path in this triangle is defined as a sequence of n circles, starting from the top row, moving to one of the two circles directly below, and concluding at the bottom row.

Here's an example with n = 6, along with a ninja path containing two red circles.

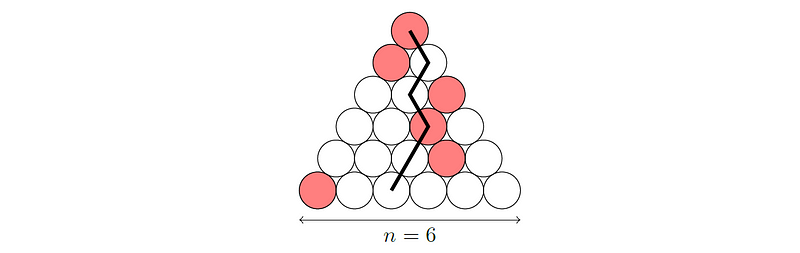
The challenge is to determine the maximum value of k such that within each Japanese triangle, there exists a ninja path including at least k red circles. The first few components of the problem are straightforward:

1. Structure of the Japanese triangle
2. Presence of one red circle per row
3. Definition of a ninja path

The complexity arises with the requirement to find the largest k, ensuring that regardless of the triangle's configuration, a path with k red circles can always be found.

Chapter 3: Initial Thoughts and Strategy

To approach this, we should consider the worst-case scenario—where identifying a path through multiple red circles is particularly difficult.

For instance, envision a scenario where half the red circles are placed along one diagonal, while the other half aligns on the opposite side.

In this arrangement, selecting a path on one side would mean missing out on the red circles on the opposite diagonal. The highest value of k in such a case might be estimated as n/2 + 1.

However, this initial hypothesis of the worst-case triangle turned out to be misleading. The journey to the correct solution often resembles navigating through a dark room—testing various paths until the right one is illuminated.

Chapter 4: Revisiting the Problem

The best approach for discrete math problems like this is to begin with the simplest case and progressively build upon it, looking for patterns.

• For n = 1, every triangle presents a ninja path with k = 1 red circle.
• For n = 2, every triangle has a path with k = 2 red circles.
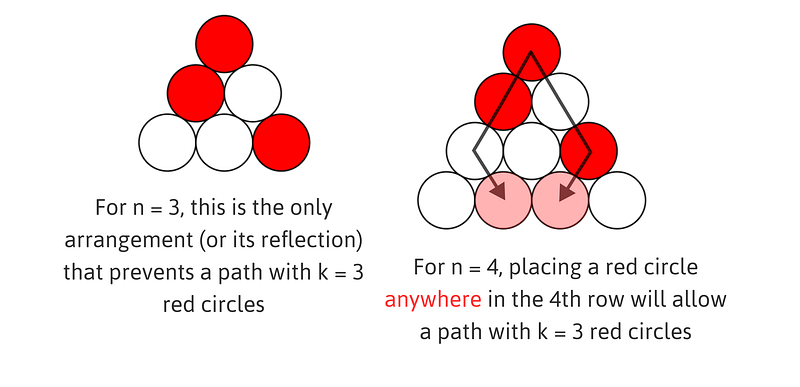
• For n = 3, the paths contain k = 2 red circles.
• For n = 4, the paths feature k = 3 red circles.

As we analyze n = 6, it becomes evident that while one arrangement allows for a path with k = 4 red circles, another configuration restricts it to k = 3.

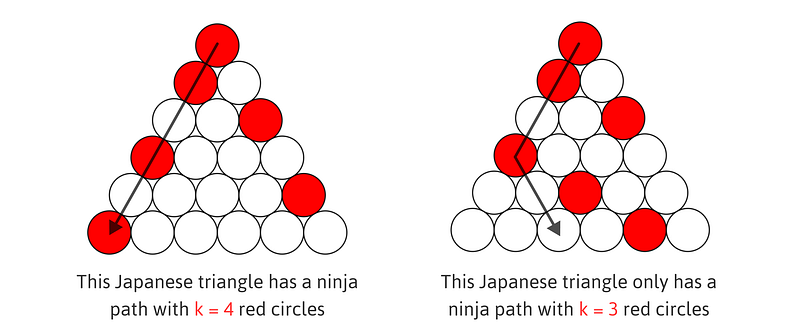
With this understanding, we can deduce that the optimal placement of red circles determines the maximum number of red circles in any ninja path.

Chapter 5: The Ultimate Conclusion

The most challenging configuration occurs when the red circles are strategically placed just out of reach from one another, ensuring that any ninja path can only intersect with one red circle across certain rows.

In conclusion, the solution hinges on the highest power of 2 less than n, allowing us to express this relationship mathematically as:

k = [log2(n)] + 1

This formula signifies that for any given Japanese triangle, there exists a ninja path containing at least this many red circles.

Explore the video titled "NICEST IMO Problem Ever? Ninja Says Yes! (IMO 2023 P5)" for further insights into this engaging problem.

Additionally, check out "International Math Olympiad, IMO 2023, Problem 5" for a comprehensive walkthrough of the solution.