Chapter 1: Introduction to Graphs

In a previous discussion, I covered the fundamentals of graphs, particularly focusing on undirected graphs.

Chapter 2: Understanding Directed Graphs

Unlike undirected graphs, which have a single concept of connectedness, degree, and neighborhood set, directed graphs introduce dual concepts in these areas.

Degree Definitions:

To begin, we define the in-degree of a node ( i ), denoted as follows:

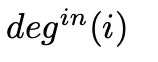
This represents the count of edges directed towards agent ( i ). Correspondingly, the out-degree of node ( i ) is defined as:

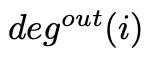
This quantifies the edges that extend away from ( i ).

Neighborhood Sets:

Next, let's examine the neighborhood sets. The in-neighbors of agent ( i ) can be expressed as:

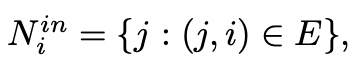
These are the other agents that transmit information to agent ( i ). On the other hand, the out-neighbors of agent ( i ) are defined as:

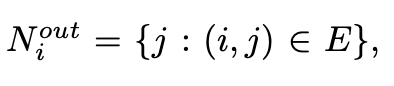
These represent the other agents to whom agent ( i ) can send information.

What Does it Mean for a Directed Graph to be “Balanced”?

Now, let’s discuss what it means for a directed graph to be considered “balanced”:

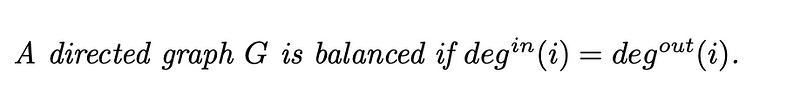
Connectedness in Directed Graphs:

Finally, we look at the two forms of connectedness applicable to directed graphs:

In the upcoming articles, I will illustrate these definitions of directed graphs to clarify these concepts further. Well-crafted visuals in science and engineering can convey complex ideas more effectively than words alone.

The first video, "Intro to Directed Graphs | Digraph Theory," provides foundational knowledge on directed graphs and their applications.

The second video, "Underlying Graphs of Digraphs | Directed Graphs, Graph Theory," explores the deeper relationships and structures within directed graphs.

Until next time,

Caleb.