Chapter 1: The Basics of the Divisibility Rule

To determine if a number is divisible by 3, you simply need to check if the sum of its digits is divisible by 3. For instance, consider the number 363279. To find out if it is divisible by 3, we sum its digits: 3 + 6 + 3 + 2 + 7 + 9 = 30. Since 30 is divisible by 3, we conclude that 363279 is also divisible by 3.

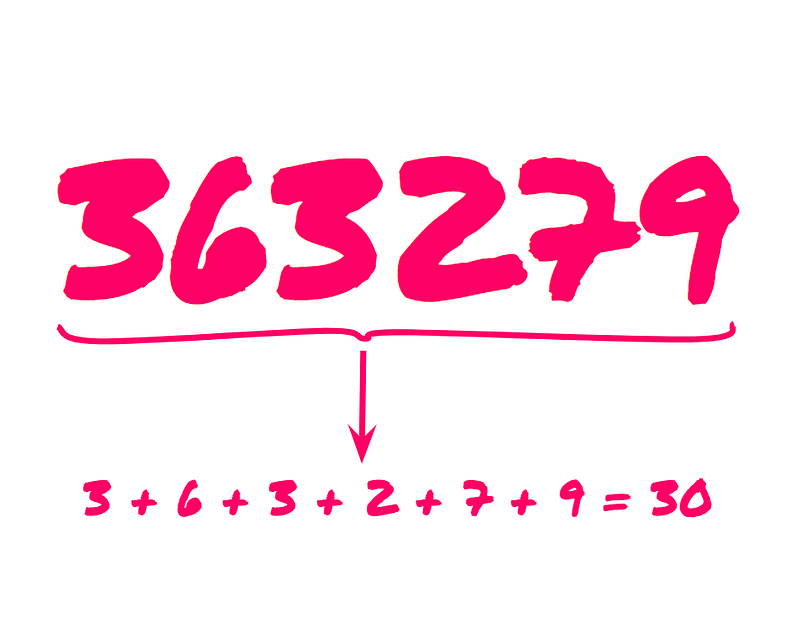
A fascinating mathematical principle, isn't it? This rule applies to natural numbers and is known as the Divisibility Rule of 3. Allow me to demonstrate its validity.

First, let's clarify what we are asserting mathematically. The assertion is that:

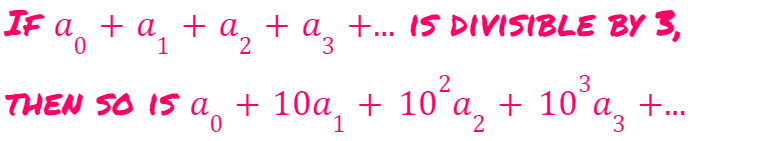
If this seems a bit perplexing, remember that a?, a?, etc., represent the digits of the number in question. For example, for the number 124, a? = 4, a? = 2, and a? = 1. Thus, 124 can be expressed as a? + 10a? + 10²a?.

Formalizing our assertion further:

Assuming that

is divisible by 3, we need to show that

is also divisible by 3.

Observe that

So, for instance, the expression 100a? + 10a? + a? can be reconfigured as (a? + a? + a?) + (100 – 1)a? + (10 – 1)a? + (1–1)a?, simplifying to (a? + a? + a?) + 99a? + 9a?.

Next, is

divisible by 3?

We already established that

is divisible, which is the basis of our assumption. Since adding two numbers that are both divisible by 3 results in another number divisible by 3, we need to confirm that

is divisible by 3. Intuitively,

represents numbers like 0, 9, 99, 999, etc., where i = 0, 1, 2, 3, etc. Since all these are divisible by 3, multiplying them by the a? term (and summing the results) will yield a number divisible by 3. But can we validate this? Yes, through Mathematical Induction.

Firstly, for our base case, we need to confirm that

is divisible by 3. Indeed, it is: 9 / 3 = 3. Thus, our base case is established.

Now, for our inductive step, we presume that

is divisible by 3 (for some natural number n). Can we demonstrate that

is also divisible by 3? Yes:

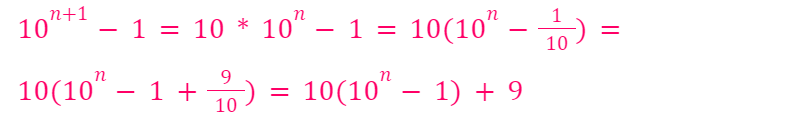
Given our assumption that

is divisible by 3, we conclude that

must also be divisible by 3. If (10? - 1) / 3 = x, where x is a natural number, then 10(10 - 1) / 3 = 10x, ensuring that if x is a natural number, so is 10x.

Since

is divisible by 3 and 9 is divisible by 3, it follows that

is also divisible by 3. Our inductive step is now complete. We have demonstrated that

is divisible by 3 for any natural number i. Hence,

is also divisible by 3. Since we assumed

is divisible by 3, we conclude

is divisible by 3, thus establishing that

is divisible by 3.

We have successfully shown that:

If the sum of a number's digits is divisible by 3, then the number itself is divisible by 3. Yet, we have not addressed whether there are numbers divisible by 3 whose sum of digits is not.

Are there such numbers? No, there are none, and the proof is quite fascinating.

We aim to demonstrate the converse of what we established earlier: if a number is divisible by 3, then the sum of its digits must also be divisible by 3.

Assuming

is divisible by 3, we have already shown that

is divisible by 3. Moreover,

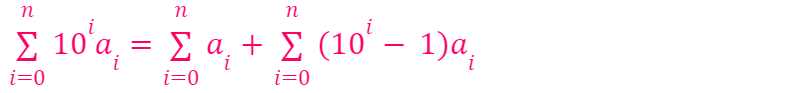
and we assumed

is divisible by 3.

For a natural number, being "divisible by 3" implies that you can repeatedly subtract 3 until you reach zero. Any natural number divisible by 3 can be expressed as 3x, where x is a natural number. If we subtract another number divisible by 3 from it, the result remains divisible by 3. Thus, 3x - 3y = 3(x - y).

What is the significance of this? Because

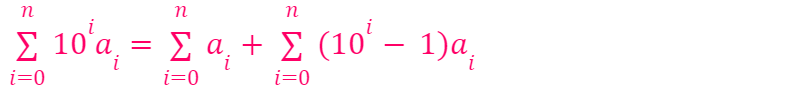
implies

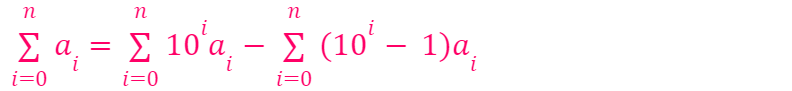
Since we have demonstrated that both terms on the right are divisible by 3, the term on the left must also be divisible by 3. Thus,

is divisible by 3, which is the desired outcome!

By combining both proofs, we conclude that

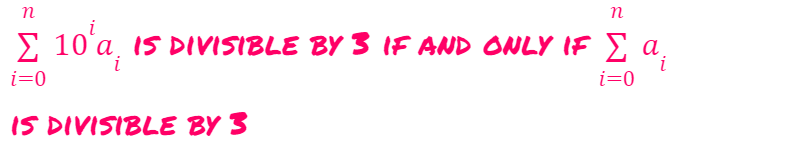
In essence, a number is divisible by 3 if and only if the sum of its digits is also divisible by 3. Quite intriguing, isn't it?

Thank you for reading! If you wish to support Street Science, consider contributing on Patreon.

Chapter 2: Video Resources for Further Understanding

This video titled "Divisibility Rule for 3 | Math with Mr. J" offers a detailed explanation of the Divisibility Rule for 3, making it an excellent resource for visual learners.

In the video "Divisibility Rule For 3," you'll find additional insights and explanations that complement our discussion, enhancing your understanding of this mathematical concept.