Chapter 1: Introduction to Hermite Functions

This section marks the fourth installment of our mini-series on special functions, focusing on an intriguing operator approach to tackle differential equations.

The term "Hermite functions" refers to functions discovered by the French mathematician Charles Hermite, who is also known for the Hermitian matrices. What makes these functions remarkable, and why should we care about them? Physics undergraduates will eventually encounter them in quantum mechanics, as they represent the stationary state solutions for the wave functions of the quantum harmonic oscillator. These functions constitute an orthonormal basis in function space (specifically for square-integrable functions). Beyond the importance of understanding Hermite functions themselves, there exists a fascinating operator method that can be employed to resolve their related differential equation. We will delve deeper into this in the subsequent sections.

The Hermite differential equation for the Hermite function ?_?(?) is expressed as follows:

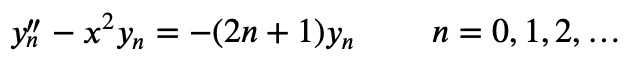
Equation 1

For those with a background in physics, you might notice that this mirrors the structure of the stationary Schrödinger equation for a one-dimensional harmonic oscillator. In order to simplify the following operator method, we will denote the derivative using the symbol ?:

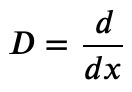
This operator acts on all terms to its right within the same "product," leading to the following outcomes:

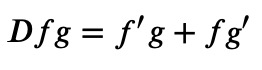
and

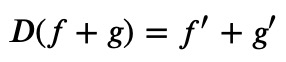
However,

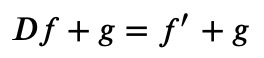
In this context, the operators (?+?) and (???) will play significant roles. Observe the result when these operators are combined:

This bears a strong resemblance to the earlier Hermite equation. Indeed, we can insert it:

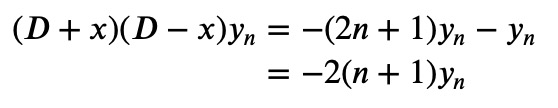
Equation 2

We can explore the effect of applying the operators in reverse order, resulting in:

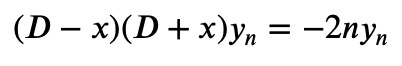
Equation 3

Now, let's examine the outcome when we apply (D-x) to Equation 2:

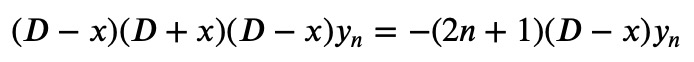
Renaming ??=(???)?_?, we can express this as:

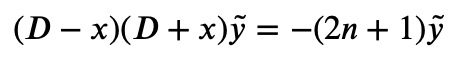
By defining the integer ? as ?=??1, we get:

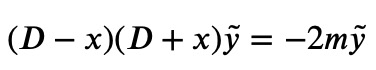
This precisely matches Equation 3, with ? and ? interchanged! Therefore, we can express:

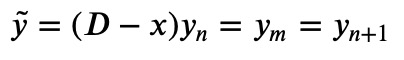
Thus, applying (???) to the ?-th function yields the (?+1)-th function! This is why ??? is termed a raising operator in quantum mechanics.

Similarly, we can apply the operator (?+?) to Equation 3. You can probably predict the effect this will have!

By renaming ??=(?+?)?_?, we have:

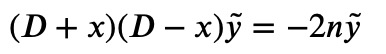
Defining ?=?+1, we arrive at:

which is precisely Equation 2, with n and m swapped. Therefore, we conclude:

In this manner, (?+?) is recognized as a lowering operator.

This is indeed fascinating, but we still need to identify the functions themselves. However, if we can determine one for a specific ?, we can derive all others using the raising and lowering operators.

The final concept to yield the solution is to impose the condition that there are no non-zero solutions for negative ?. Specifically, when we apply the lowering operator to ?_0, the outcome must be zero. Thus, we require:

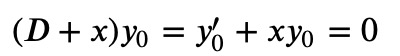
This is a straightforward problem to solve! By inspection, we can see that the solution (up to a multiplicative constant) is simply:

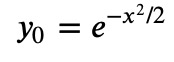
With this solution, we can derive all other functions:

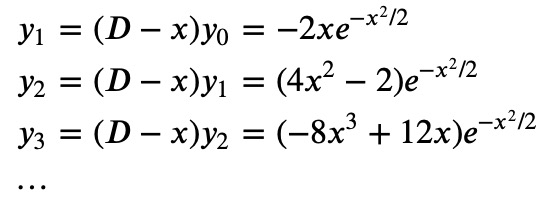
Each Hermite function is represented by the same Gaussian multiplied by a polynomial ?_? of degree ?. These polynomials are referred to as Hermite polynomials. Thus, we can visualize the Hermite functions as follows:

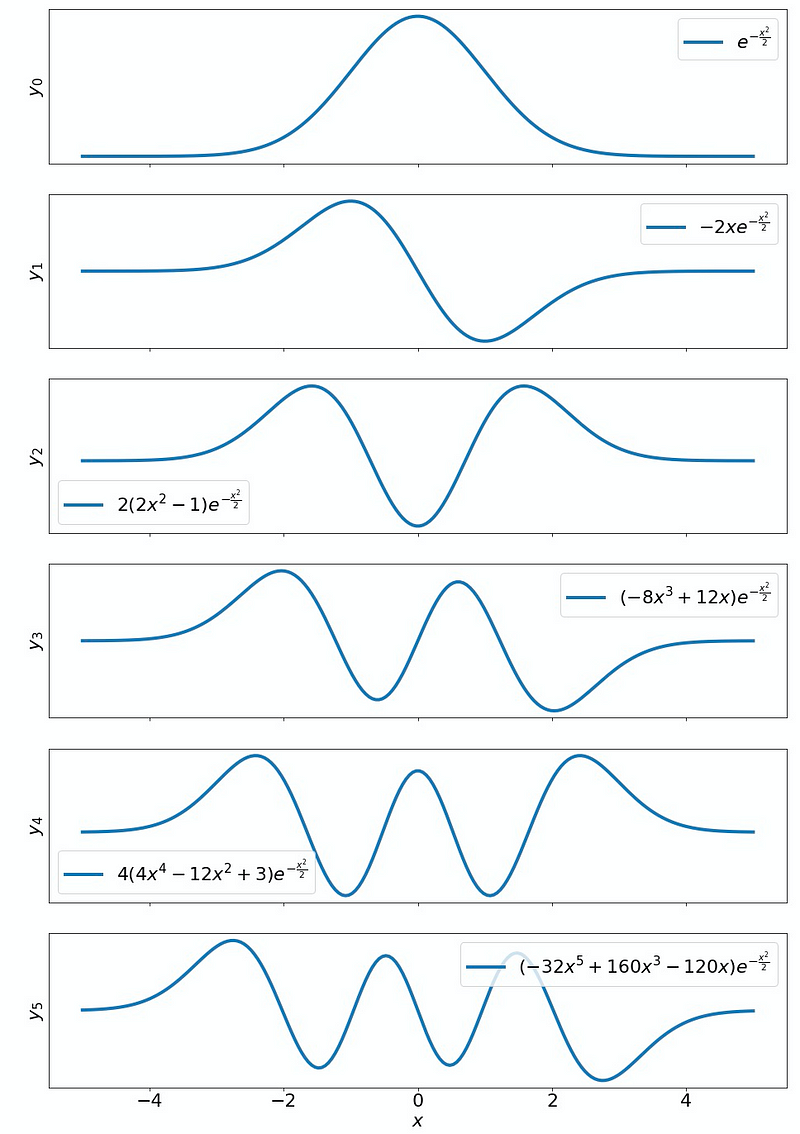
For the matplotlib code used to generate the figure, please refer to the supplementary page linked to this article.

Chapter 2: Further Exploration with YouTube Videos

To deepen your understanding, here are two insightful videos:

The first video, "Introduction to Hermite Polynomials," provides a foundational overview of these important mathematical constructs.

The second video, "Hermite Polynomial Generating Function," explores the methods for generating these polynomials effectively.

Thank you for engaging with this material!