What Constitutes Numerical Sets?

A brief overview of numerical sets: What are they? How many types exist? What are their defining features?

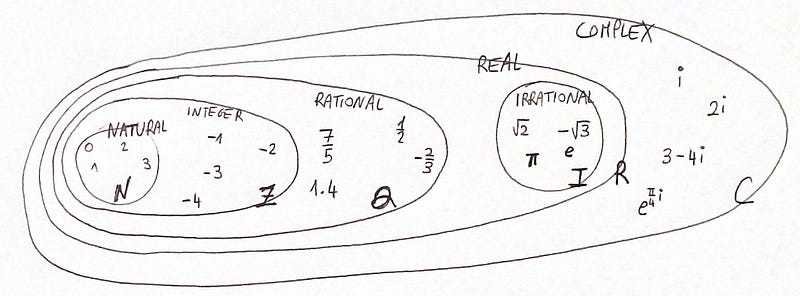
Photo credited to the author.

Rational and irrational numbers both belong to the category of real numbers. But what exactly are real numbers?

A real number can be expressed with either a finite or an infinite series of decimal places. For instance:

• The number “2” is a real number because it can be represented as 2.0 (finite decimals) or 2.000000… (infinite decimals).
• The square root of 2 is also a real number, represented as 1.414213562… (infinite decimals).

Most familiar numbers you encounter fall under the category of real numbers. However, complex numbers do not qualify as real numbers. To gain a deeper understanding, please refer to the accompanying image.

So, what are complex numbers? For further reading, check the linked article. A more comprehensive piece on complex numbers will be published soon.

Rational Numbers Explained

So, what exactly is a rational number? First and foremost, it is a real number. Feel free to revisit the definition of a real number if needed.

Secondly, a rational number can be expressed as a ratio of two integers. In mathematical terms, this format is referred to as a fraction.

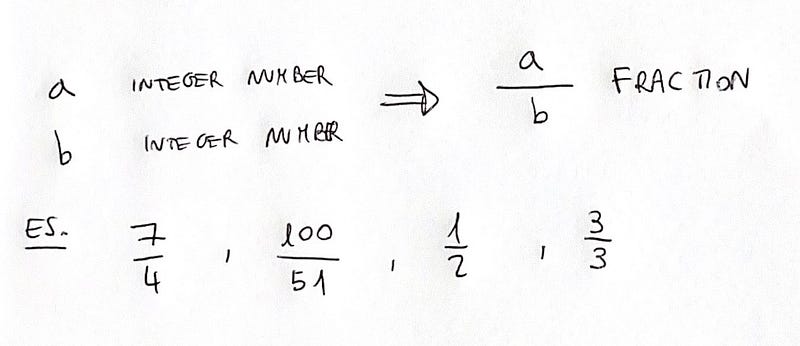
Photo credited to the author.

A rational number can be represented as a fraction or can be converted into such a form. Here are some examples:

• “4/7” qualifies as a rational number since it is a fraction formed from the integers 4 and 7.
• “-8/9” is similarly a rational number for the same reasons stated earlier.
• The number “2” is also rational as it can be expressed as a fraction: 2 can be rewritten as 4/2, 6/3, 8/4, 10/5, etc.
• However, the square root of 2 is not a rational number because it cannot be expressed as a ratio of two integers.

Irrational Numbers Defined

What about the square root of 2? As previously mentioned, it is a real number that can be expressed with an infinite number of decimal digits, yet it cannot be represented as a fraction.

An irrational number is defined as a real number that cannot be expressed in fractional form. Therefore, the square root of 2 is classified as an irrational number.

Understanding Fractions

It’s crucial to grasp the definition of a fraction: it must be a ratio of two integers.

Consider the number “pi” (3.14… etc.). This is also an irrational number. Remember, integer numbers are themselves rational, meaning the set of integers is included within the realm of rational numbers. Thus, integers cannot be classified as irrational.

With this understanding, we can also comprehend why “pi/2” is not a fraction; it comprises a non-integer (pi) and an integer (2).

What are Numerical Sets?

In conclusion, we have explored various numerical sets and their characteristics.

You may also find interesting:

What are Complex Numbers?

This section will introduce you to complex numbers—what they are, how they are defined, and some of their properties and examples.

Thank you for reading my article. I hope this information has enhanced your understanding of these mathematical concepts. Feel free to follow me and subscribe below with your email to be notified of my latest daily articles.

The first video, titled "What is the Difference Between Rational and Irrational Numbers," offers an engaging explanation of the concepts discussed.

The second video, "Rational and Irrational Numbers," provides additional insights into the topic and is recommended for further learning.