Exploring the Intersection of Biology and Fourier Transforms
Written on
Chapter 1: The Biological Basis of Computational Models
In recent years, there has been a growing trend to develop mathematical and computational models inspired by biological systems. These systems have been meticulously refined by evolution to optimize their functionality and survival, making them an excellent source of inspiration for our computational approaches. Essentially, we humans have become the solution to many of our own computing challenges.
A quintessential example of this is the perceptron found in artificial neural networks, which is designed for binary classification. This model is based on the way a biological neuron processes incoming action potentials from other neurons, integrating information similarly at its "axon hillock."
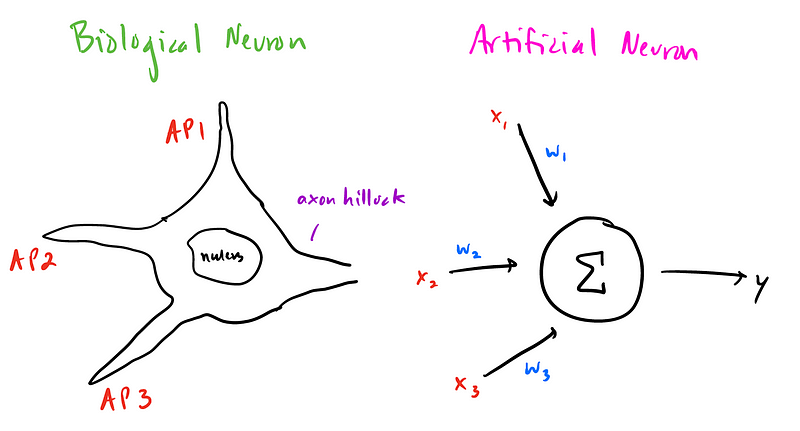
Analogies:
- Action Potential (AP) = Inputs (x1, x2, …)
- Axon Hillock = Summation
- Neurotransmitter Strengths = Weights (w1, w2, …)
Section 1.1: Understanding Fourier Transforms
Fourier transforms fundamentally involve the transition from one domain to another, which can also be described as a change of basis. In quantum mechanics, this refers to the shift from position space to momentum space. Similarly, in electrical engineering and signal processing, this transformation typically occurs from the time domain to the frequency domain.
Fourier transforms hold significant power in signal processing, as they enable us to isolate various components across different frequencies that combine to recreate the original signal. Intriguingly, our auditory system performs this complex mathematical operation without the need for numerical representation!
Section 1.2: The Cochlea and Sound Processing
The cochlea, a spiral-shaped structure located within our ears, plays a pivotal role in this process. It contains numerous hair cells, each tuned to specific resonant frequencies. When sound waves, composed of various frequencies, enter the ear, these hair cells selectively respond to different waveforms. Essentially, the cochlea constructs a frequency spectrum from the incoming time-dependent signal.
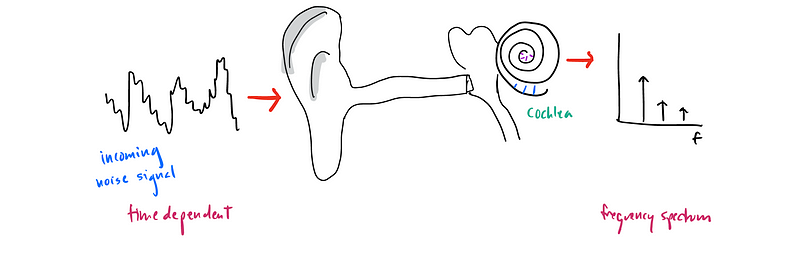
The inner ear does not lose any information from incoming sounds; rather, it finds an alternative method to represent them. Don't forget to express your appreciation for this knowledge by giving a round of applause to those sharing insights! :)
Chapter 2: Practical Applications of Fourier Transforms
The first video titled "Lecture 4 | The Fourier Transforms and its Applications" provides an in-depth look at the principles and uses of Fourier transforms in various fields.
The second video, "Real-life Applications of Fourier Transforms" by Sheamol Obeda, explores how Fourier transforms are applied in practical scenarios.