Exploring the Intriguing World of Mersenne Primes
Written on
Chapter 1: The Allure of Prime Numbers
Prime numbers have captivated mathematicians for centuries. They occupy a unique position on the spectrum of chaos and order, often resisting predictability, yet revealing patterns under certain perspectives. To better comprehend these enigmatic numbers, mathematicians have developed various classifications, among which Mersenne Primes stand out as particularly intriguing.

Section 1.1: A Glimpse into Marin Mersenne
These special primes are named after Marin Mersenne, a French monk who lived from 1588 to 1648. Mersenne was a polymath, contributing to diverse fields, notably music theory, and he is credited with publishing foundational works on vibrating strings. Most importantly, he was the first to systematically define and catalog a specific category of prime numbers, now known as Mersenne Primes.
The definition of a Mersenne Prime is straightforward. It is a prime number that can be expressed in the form:
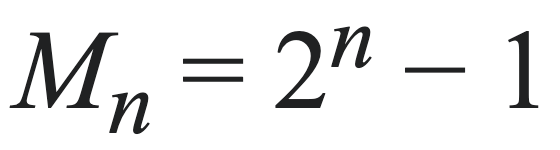
for any integer n. Not every integer n results in a prime number. For instance, with n = 4, M(n) = 15, which is not prime. Numbers of this type are referred to as Mersenne Numbers. For M(n) to yield a prime, n itself must be prime. However, having n as prime does not guarantee that M(n) will also be prime. For example, when n = 11, M(n) = 2047 = 23*89. Below is a list of n values that Mersenne discovered to yield prime numbers, though his exploration was restricted by the technology of his time.
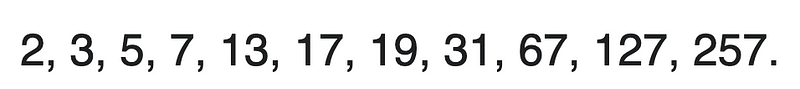
Section 1.2: The Mysteries of Mersenne Primes
Numerous open questions about Mersenne Primes remain. It is still uncertain whether there are infinitely many Mersenne Primes. Their prominence is largely due to their crucial role in the pursuit of the largest known prime number. Let's explore why they are so vital to this quest.

#### The Great Search
In the realm of mathematics, the pursuit of larger prime numbers has been a long-standing endeavor. The rise of computers has significantly accelerated this search. Since the 1990s, the "Great Internet Mersenne Prime Search" (GIMPS) has spearheaded efforts to uncover larger Mersenne Primes. Utilizing distributive computing, anyone can download their software and contribute a small fraction of their computer's processing power to test new Mersenne Primes.
As of the time of writing, GIMPS has rigorously tested all exponents up to 68,874,199 multiple times and has at least once tested up to 117,776,773. Each candidate Mersenne Prime must undergo extensive testing before a conclusion is reached. The search for Mersenne Primes is particularly advantageous due to their unique properties. As potential primes grow larger, the time required for testing increases. However, the Lucas–Lehmer primality test, which is exclusively applicable to Mersenne Numbers, is far more efficient. Furthermore, we know the exponent must also be a prime number.
The GIMPS initiative is impressive, with over 20,000 computers participating in the project. In 2018, Patrick Laroche discovered the most recent Mersenne Prime, marking the 51st known Mersenne Prime, which has an exponent of 82,589,933 and consists of over 20 million digits. GIMPS offers cash rewards ranging from $3,000 to $50,000 based on the size of the discovered prime, inviting others to join the effort both for the prizes and the historical significance of the endeavor.
Section 1.3: The Connection to Perfect Numbers
While Mersenne Numbers are often associated with their namesake, Marin Mersenne, their significance extends deeper into mathematical history due to their link to perfect numbers. The relationship between perfect and Mersenne numbers has been recognized for millennia, dating back to Euclid’s seminal work, "Elements." To appreciate this connection, we must first define what a perfect number is.
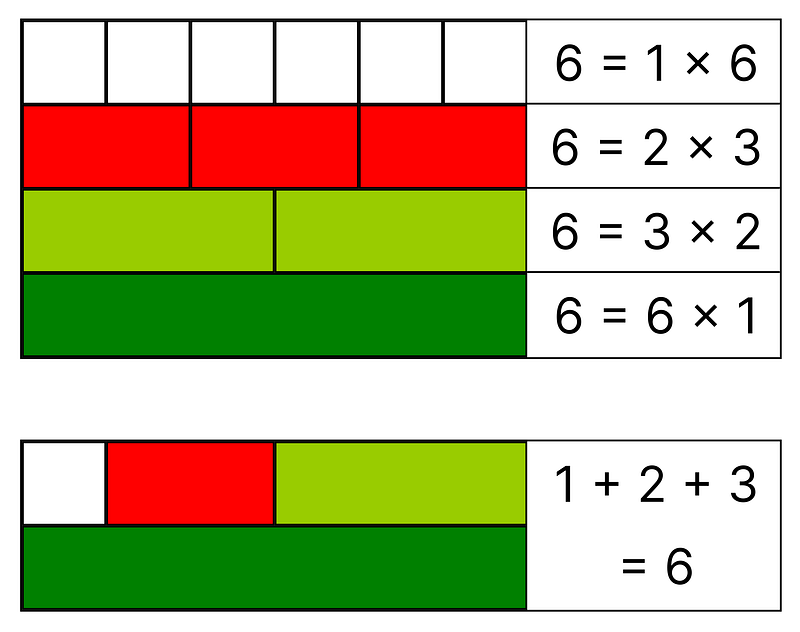
A perfect number is one that equals the sum of its proper divisors. Proper divisors are numbers that divide a given number without including the number itself. For instance, the divisors of 6 are 1, 2, 3, and 6, but the proper divisors are 1, 2, and 3. The number 6 is the smallest known perfect number, as 1 + 2 + 3 = 6. The next smallest perfect number is 28, as 1 + 2 + 4 + 7 + 14 = 28. These numbers increase quickly in size, with the subsequent smallest being 496 and 8128.
Debate persists regarding the existence of any odd perfect numbers. Although many mathematicians have argued against their existence, it remains an unresolved question in mathematics.
To explore their link to Mersenne Primes, we turn to Euclid’s proof from the 4th century BC, which established that if

is a prime, then
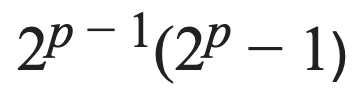
is a perfect number. For example, when p = 2, 2² - 1 = 3, which is prime. Hence, 2¹(2² - 1) = 6. This relationship holds for all values of p that yield a Mersenne Prime. Later, in the 18th century, Euler demonstrated that all even perfect numbers conform to this format, now referred to as the Euclid-Euler theorem. In essence, every even perfect number can be paired with a Mersenne Prime, revealing a profound relationship between these two types of numbers.
Going Further
I hope this exploration has enlightened you! Mersenne primes offer a rich and fascinating area of mathematical study that has been evolving for centuries. This overview barely scratches the surface of the theories surrounding them. For further reading, I’ve included links below for more information.
You can access the GIMPS homepage here. Even if you don't wish to participate, it offers intriguing insights!
The OEIS pages on perfect numbers and Mersenne Primes provide a wealth of knowledge.
For those eager to delve deeper into the mathematical theories behind Mersenne Primes, I highly recommend this free online textbook focused on number theory. It’s an invaluable resource!