Early Life

Euler was born in Basel on April 15, 1707. His father was acquainted with the Bernoulli brothers, particularly Johann Bernoulli (1667–1748), who was then one of the world's foremost mathematicians. Johann played a crucial role in shaping Euler's mathematical journey.

In 1723, Euler earned a Master's degree in philosophy—a reflection of the scientific studies of the time—while also pursuing Theology. During this period, he received tutoring from Johann Bernoulli, who soon recognized Euler’s mathematical talent and persuaded his father to allow him to focus on mathematics instead of theology.

In 1727, Euler participated in the Paris Academy Prize Problem competition, tasked with determining the optimal placement of masts on a ship. He secured the second position, narrowly missing first place to Pierre Bouguer, despite having never set foot on a ship before. Euler would eventually win this competition twelve times. His attempts to secure a position at the University of Basel were unsuccessful, a significant misjudgment by the institution. Fortunately, Daniel Bernoulli, Johann's son, helped Euler gain a position at the Academy of Sciences in St. Petersburg shortly thereafter.

Exploring Infinity

In the mid-17th century, mathematicians faced a formidable challenge: to find the precise value of an infinite sum, often referred to as a series.

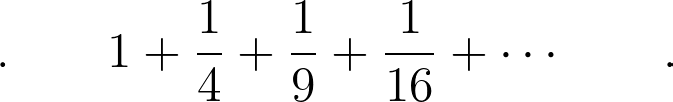
As one calculates more terms, the sum approaches a specific value, approximately 1.644934. This phenomenon is known as convergence, a concept understood by mathematicians of the era. The challenge lay in deriving a "closed-form expression" for this series.

You may wonder, how can one sum something infinite? Formally, an infinite series is defined as a limit. Picture painting a wall: each day, you paint half of the remaining area. Initially, you cover half the wall, then a quarter of what's left, and so forth. Two significant points emerge from this method:

1. You cannot exceed the wall's total area.
2. If you keep painting, you will eventually cover more than any arbitrarily small fraction of the wall.

Thus, if you had infinite days to continue painting, you would ultimately cover the entire wall! This concept illustrates convergence, allowing us to express it as:

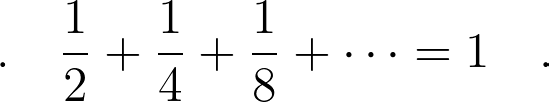
Here, the ellipsis indicates continuation towards infinity. As we delve into famous series, we will explore a significant challenge known as the Basel Problem, which stumped several prominent mathematicians, including the Bernoulli brothers and Leibniz.

Before unveiling Euler’s groundbreaking proof, we need some context regarding infinite series. Euler frequently employed infinite series in his work, particularly a type called the Taylor series.

Understanding the Maclaurin Series

A power series can be thought of as an infinite polynomial:

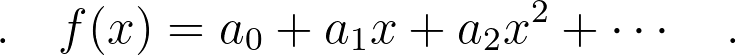
Suppose you have a function f. Even if f isn’t a power series, we can approximate it as one by identifying coefficients. By evaluating the function at specific points, we can derive the coefficients necessary for constructing the series.

To extract the nth coefficient, we differentiate the series multiple times and evaluate it at zero. Dividing by n! accounts for the reduced power with each differentiation. This reveals a general formula for the coefficients in a power series, establishing the Maclaurin series expansion:

When this series converges, it equals the function f. With this foundation, we can examine Euler’s approach to the Basel Problem.

Euler's Resolution of the Basel Problem (1734)

Euler began with the Maclaurin series expansion of the sine function:

Dividing this series by x, he derived a new expression:

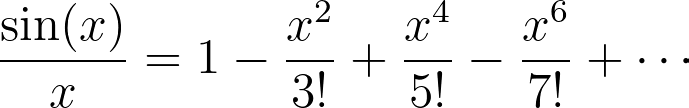
Euler, ever the innovator, recognized that the left side could be viewed as an infinite polynomial and applied the Fundamental Theorem of Algebra, which states that polynomials can be factored into linear components.

He hypothesized that this theorem also applied to infinite polynomials like the sine series. Assuming this is true, he identified the zeros of the function as the multiples of π:

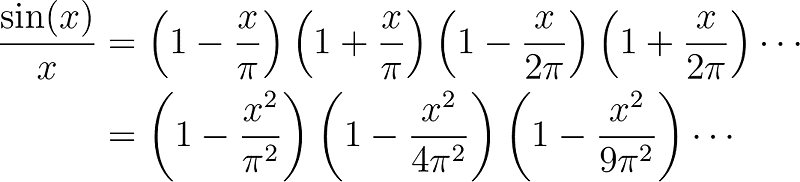
By multiplying these terms, he ingeniously eliminated the square numbers in the denominator, simplifying his calculations.

He compared this with the earlier Taylor expression and concluded that the constants of both expressions must be equal, yielding:

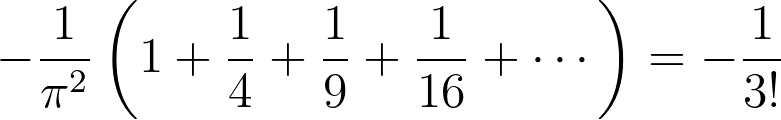
This elegant proof established that:

This revelation catapulted Euler into fame, as it bridged the realms of squares and circles—a connection previously unrecognized. Euler extended his investigations to the sums of higher powers, although he could not derive a closed-form expression for odd powers, leaving an enduring mystery in mathematics.

Later, the assertion that the sine function could be expressed as an infinite product over its zeros would require a more profound theoretical underpinning, which was eventually provided by Karl Weierstrass in the 19th century.

A Gateway to Analytical Insights

Euler's fascination with these series led him to define a real-valued function:

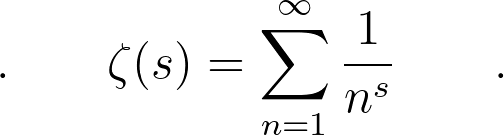
This function is valid only for s > 1, with the Basel Problem specifically corresponding to s = 2. Euler then introduced the Euler product, an expression that connects sums over natural numbers and products over prime numbers:

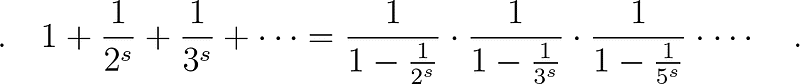
This result would lay the groundwork for Analytic Number Theory, where properties of numbers are explored through both real and complex analyses.

Euler's work illuminated the relationship between additive and multiplicative structures in mathematics, a connection that would not fully reveal its significance until the advent of the Riemann Zeta Function, named after Bernhard Riemann due to its complex implications.

The Riemann Hypothesis—concerning the distribution of prime numbers and their relationship to the zeros of the zeta function—remains one of mathematics' most profound mysteries. The resolution of this hypothesis promises not only a million-dollar prize but also eternal recognition alongside history's greatest mathematicians.

As we continue to unravel Euler's legacy, we will explore one of mathematics' most beautiful equations and delve into the geometric reasoning behind the multiplication of negative numbers.

Conclusion

The study of Euler's works remains an unparalleled foundation for understanding various mathematical disciplines, proving invaluable through the ages. ~ Gauss

In this introductory video, we explore Euler's "Introductio in Analysin Infinitorum," providing insights into his groundbreaking contributions to mathematics.

This video provides detailed explanations of Euler's calculation of the exact sum of the p-series for p=4, illustrating his profound impact on calculus.