Chapter 1: Introduction to the Algebra Puzzle

Welcome to the ninth installment of our tricky algebra problem series! In this entry, we are tackling another relatively straightforward yet deceptively tricky equation. The problem at hand is:

[2^(3x)] ? (2^x) = 336

where x ? R

Your mission is to determine the value of ‘x’. This puzzle does not hide any complexities; it’s genuinely easier than it appears. Now that you’re aware of this, how would you approach solving it?

Spoiler Alert

I will be revealing the solutions to this equation shortly. If you prefer to solve it independently, I suggest pausing here to give it a try. Once you’ve attempted it, feel free to continue reading to compare your method with mine.

Section 1.1: Setting Up and Simplifying the Equation

Upon examining the equation, it becomes clear that both terms on the left share a common exponent of ‘x’. To simplify our work, let’s introduce a new variable ‘t’ defined as:

t = 2^x

This allows us to rewrite the original equation as follows:

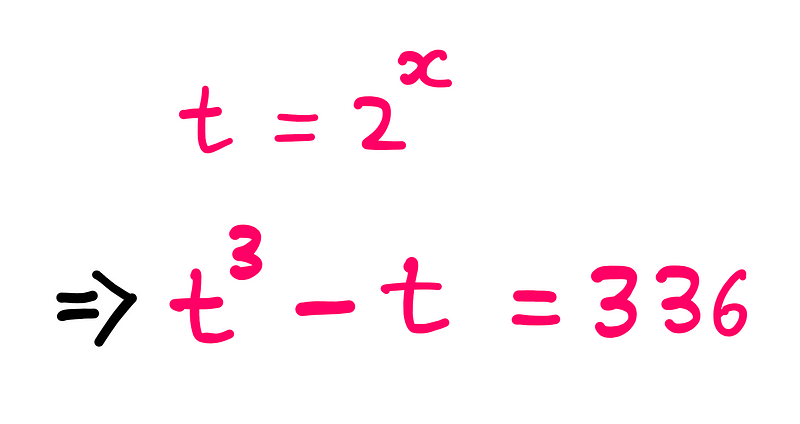
Next, we can factor out ‘t’ from the left-hand side:

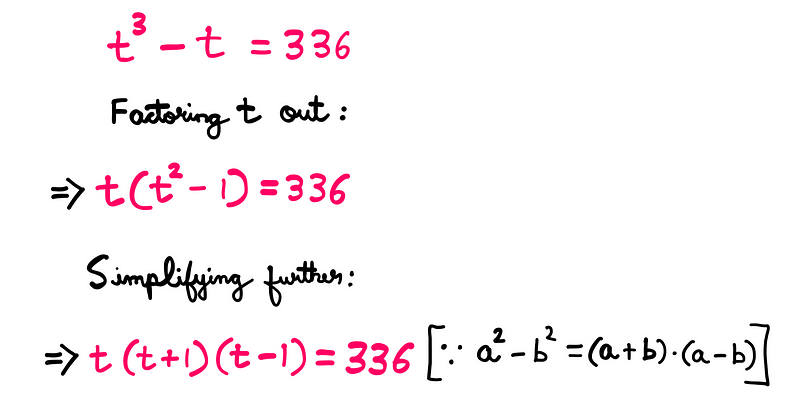
Notice how this equation leads directly to one of the roots we are seeking. If you’re not seeing the pattern yet, don’t worry—let’s delve deeper.

Section 1.2: Discovering the Pattern and Solving for ‘t’

Let’s rearrange the multiplicative terms on the left side:

(t - 1)*t*(t + 1) = 336

By considering integers (a subset of real numbers), we can infer that the left side represents the multiplication of three consecutive integers. The right side is simply a three-digit number, suggesting that by testing a few combinations of integers below 9, we should be able to find our first root. Let’s see:

2*3*4 = 24

3*4*5 = 60

4*5*6 = 120

5*6*7 = 210

6*7*8 = 336 — Bingo!

We have determined that 7 is a root for our parameterized expression. Thus, the equation can be expressed as follows:

The next step involves reverse-engineering the missing expression to keep the equation valid. Since we have t³ on the right, we can deduce that the missing expression must include t².

Subsection 1.2.1: Completing the Equation

As we deduce the missing terms, we arrive at the final expression:

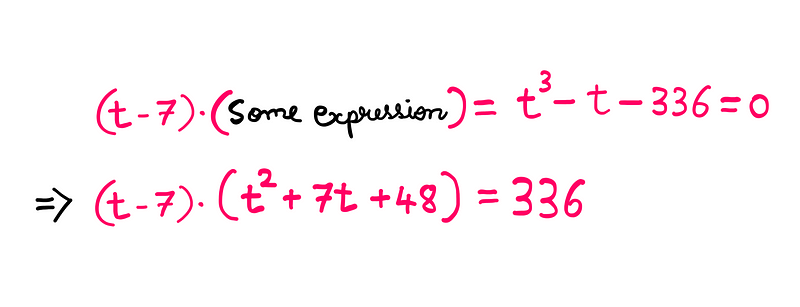
To find the remaining roots, we’ll need to solve the quadratic expression we’ve established. However, before proceeding, let’s check if it has real roots by calculating the discriminant (Δ):

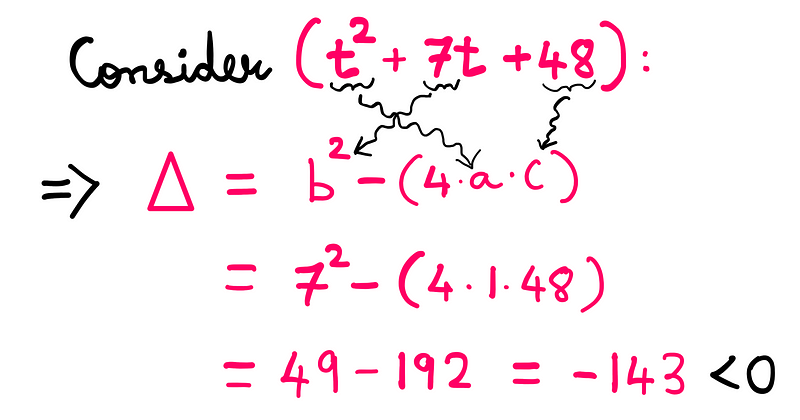
Since the discriminant is negative, we conclude that (t² + 7t + 48) does not have real roots. Thus, (t = 7) is the sole viable root.

Reader Insight

A valuable observation from reader Shevach Riabtsev highlights that the function (t-1)t(t+1) is monotonically increasing for t > 1, confirming a single solution for (t-1)t(t+1) = 336.

Chapter 2: Finding the Final Solution

Before we can celebrate, we must revert to our original variable and find ‘x’. Since we know that t = 2^x, we can set up the equation:

2^x = 7

To solve for ‘x’, we will utilize logarithms. By applying the natural logarithm to both sides, we get:

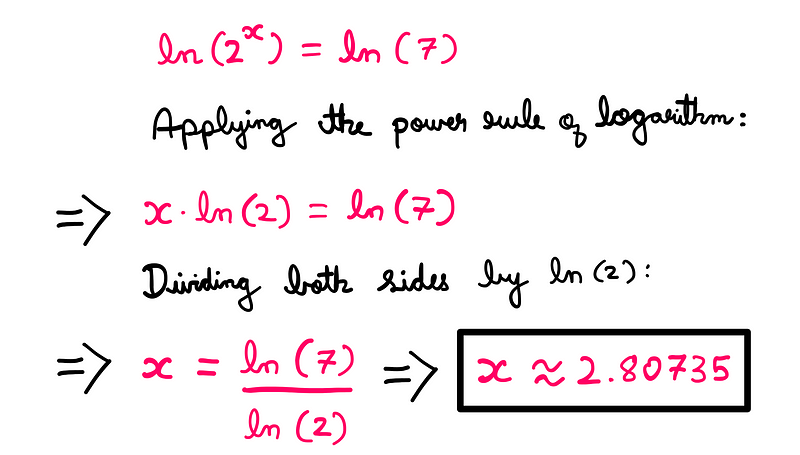
And there we have it! This concludes our exploration of this tricky algebra problem. I hope you enjoyed the process as much as I did!

Chapter 3: Engaging with Video Content

To further enhance your understanding of algebraic solutions, check out the following videos:

The first video, Equation Solving | 97% FAILED to answer this question | Algebra, delves into the intricacies of equation solving and will provide additional insight into similar problems.

The second video, Tricky Algebra Question | 97% won't get this, challenges viewers with perplexing algebra questions, making it a perfect companion to this discussion.