Newton's Cannonball: The Path from Thought Experiment to Orbits
Written on
Chapter 1: The Power of Thought Experiments
Thought experiments serve as crucial instruments in various disciplines such as science and philosophy. Historically, thinkers have utilized them extensively; notable examples include Galileo's assertion that different masses fall simultaneously and Einstein's conceptual chase of a beam of light, which was pivotal in shaping his special theory of relativity.
These mental exercises allow us to delve into scenarios that can't be physically tested. An illustrative case is Schrödinger’s cat, a thought experiment that presents a cat existing in a state of both life and death, thereby elucidating the concept of quantum superposition—something that is not observable in everyday experiences.
As Ernst Mach stated:
> “Our own ideas are more easily and readily at our disposal than physical facts. We experiment with thought, so as to say, at little expense. It shouldn’t surprise us that, oftentimes, the thought experiment precedes the physical experiment and prepares the way for it… A thought experiment is also a necessary precondition for a physical experiment. Every inventor and every experimenter must have in his mind the detailed order before he actualizes it.”
Mach emphasized that the fundamental technique of a thought experiment mirrors that of physical experimentation, particularly through the method of variation. By altering the conditions continuously, we expand the applicability of an idea related to those conditions.
Section 1.1: Newton's Hypothetical Cannonball
In the 17th century, Isaac Newton engaged in a thought experiment regarding the Moon's circular orbit around Earth. Picture a cannonball being shot horizontally from an elevated location. In a vacuum, this cannonball would travel in a straight line at a constant speed. However, due to Earth's gravitational force, it begins to curve downward, tracing a parabolic path toward the ground.
Now envision increasing the cannonball's initial velocity. It will still descend but will cover a greater horizontal distance before impacting the Earth. Newton realized that if this initial velocity were sufficiently high, the cannonball would fall toward the Earth at a rate matching the Earth's curvature, resulting in an orbit. He concluded that the Moon's circular trajectory is a product of its tangential speed combined with the gravitational pull exerted by Earth.
The principles of gravitational attraction and motion illustrated by this thought experiment were first articulated in Newton's groundbreaking work, "Philosophiae Naturalis Principia Mathematica," published in 1687. In this text, he introduced his three laws of motion and his law of universal gravitation, fundamentally transforming our comprehension of the physical universe and laying the groundwork for modern physics.
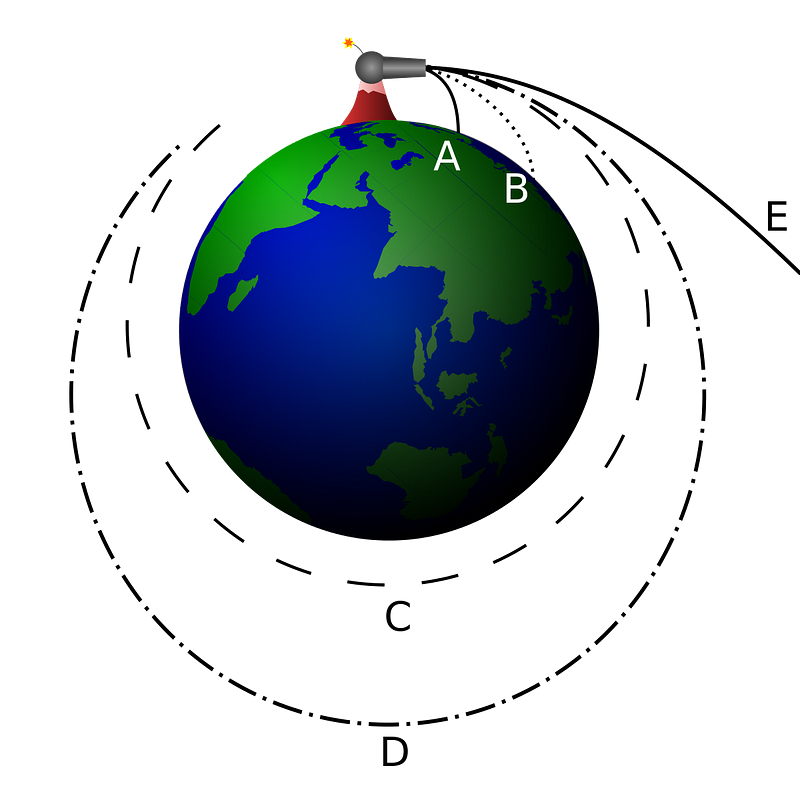
This diagram depicts the various trajectories a cannonball could take when fired from a mountain, depending on its initial speed. If the speed is low, it follows trajectory A and falls directly to Earth. With a slightly higher velocity, it lands at point B, and with the right speed, it orbits as in trajectory C. A greater speed leads to an elliptical path (trajectory D), while an extremely high speed allows it to escape Earth's gravitational influence altogether (trajectory E).
Escape velocity refers to the minimum speed needed for an object to break free from a celestial body's gravitational grip. This speed varies with the mass of the celestial body and the distance from its center. An object launched from Earth at less than the escape velocity will eventually return due to gravitational attraction, while one launched at or above this threshold will continue to move away.
For Earth, the escape velocity is approximately 11.2 kilometers per second (6.95 miles per second), whereas the Moon's escape velocity is significantly lower at around 2.38 kilometers per second (1.48 miles per second).
This thought experiment, often termed "Newton's cannonball," clarifies the intricate relationship between gravity and motion, illustrating how gravitational forces govern the paths of moving objects. By conceptualizing a cannon firing from a mountain, Newton distilled the complexities of motion and gravity, enabling him to formulate his laws of motion and universal gravitation—cornerstones of classical mechanics that reshaped our scientific understanding.
The first video, titled "ExoDet1C: Newtonian Orbits | 1. Celestial Mechanics | EXOPLANET DETECTION," explores the principles of Newtonian orbits and their applications in celestial mechanics.
The second video, "ExoDet1B: Newtonian Gravity | 1. Celestial Mechanics | EXOPLANET DETECTION," delves into the foundational concepts of Newtonian gravity and its significance in understanding celestial bodies.
Thank you for engaging with this exploration. Your thoughts and feedback are welcome—feel free to share your insights! If you wish to express your appreciation, consider giving this piece a clap or treating me to a coffee. ☕