Chapter 1: Introduction to the Problem

This particular challenge emerged as the opening question of the 2024 Australian Mathematical Olympiad. Typically, the first problem is crafted to be the most straightforward among the six presented. However, I personally found this one to be unexpectedly intricate.

The authors of the problem opted to clarify the concept of n! factorial, which I find somewhat humorous—it's unlikely that any participant in this prestigious National Olympiad would be unfamiliar with factorials! Yet, it’s worth noting that factorials are not included in the 7–10 Mathematics Curriculum.

Moving forward…

Chapter 2: Exploring Solutions

As is my custom, I start by testing small values to find a solution. Fortunately, we don't have to look far! Substituting m = 1, k = 1, and n = 2 yields:

1! + 1! = 1! × 2!

This holds true since 2! = 2. We can also generalize this by setting m = k while keeping n = 2:

k! + k! = k! × 2!

This equation is valid for any k, as doubling k! is equivalent to adding it to itself. Thus, we have an infinite set of solutions of this form.

However, we must ask: are these the only solutions available?

To investigate algebraically, we can rearrange the k! terms and factor them:

m! + k! = k! × n!

m! = k! × n! - k!

m! = k! (n! - 1)

This expression proves valuable as it contains a factorial on both sides, with an additional factor on the right. It is indeed quite useful and will allow us to solve the problem effectively in just a few steps. Yet, I must admit, I pondered over this for far too long before realizing its significance!

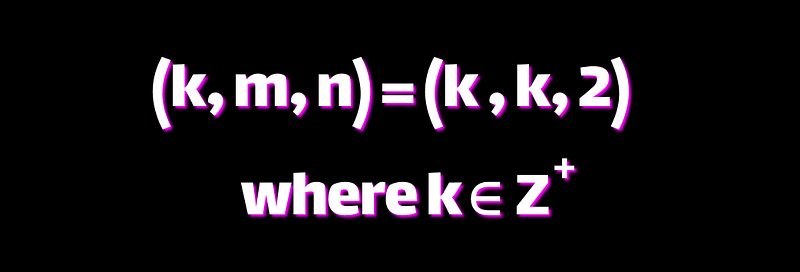
The crucial insight is that all factorials starting from 2! are even. Consequently, for n > 2, the term (n! - 1) must be odd.

Both sides of the equation must remain even, indicating that we need to multiply k! by an odd number to obtain m!. This implies that m must exceed k, as (n! - 1) will be greater than 1 unless n = 2 (which we have already addressed).

Moreover, m cannot be even; otherwise, (n! - 1) would need to include an even factor larger than k. Thus, m must be odd. We can refine our conclusion further: m must equal k + 1.

For instance, if we were to seek a solution where m = 9 and k = 7, we would encounter a conflict, as 9! = 9 × 8 × 7!, necessitating a factor of 8 within the (n! - 1) term. This scenario is impossible since (n! - 1) is always odd.

Thus, we conclude that m is odd and m = k + 1.

Chapter 3: Determining the Value of n

What about n? As long as n > 2, it can be any integer, and (n! - 1) will consistently be odd. We then set k to be one less than (n! - 1), allowing the right-hand terms to combine to form a factorial: m! = (n! - 1)!

To illustrate, let’s consider n = 7. Here, 7! = 5040, leading us to set k as one less than (7! - 1), which gives k = 5038. Then, m = k + 1 results in m = 5039.

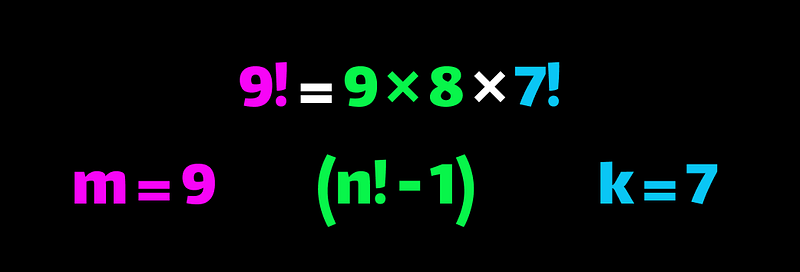
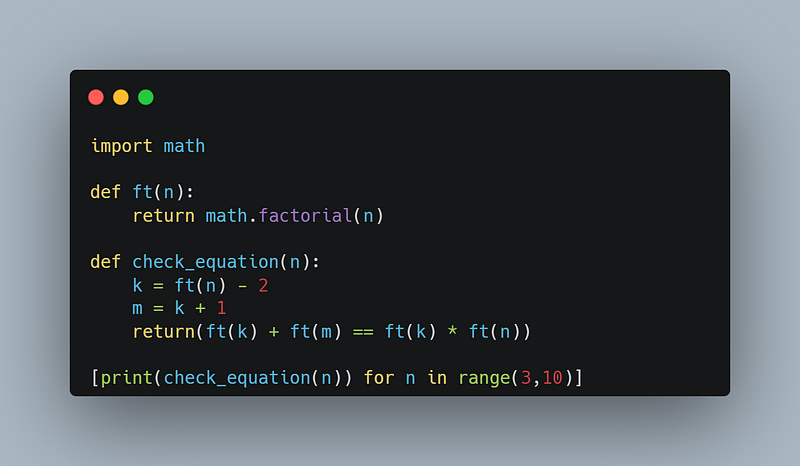
This method holds for any n > 2. I quickly checked several small n values using Python.

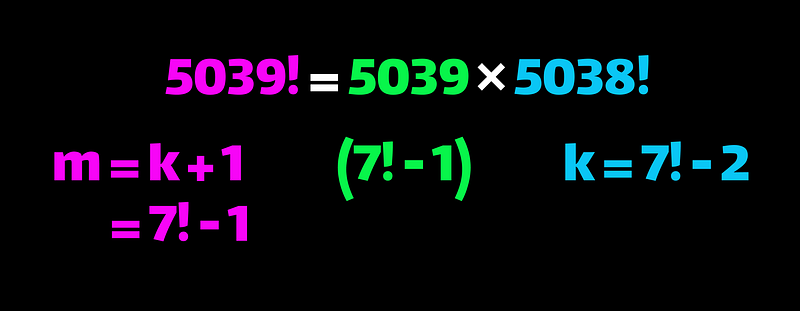
Indeed, it confirmed the validity for all n values from 3 to 9 (although the final evaluation for 9! = 362880 took some time since k! = 362878! is rather large!).

That’s the conclusion! This yields our second and final set of solutions:

Chapter 4: Additional Resources

For further insights into factorial equations, check out the following videos:

The first video, titled "Nice Factorial Equation - Can You Solve It?" offers a thoughtful exploration of similar factorial challenges.

The second video, "A Nice Factorial Equation," dives deeper into the nuances of solving factorial equations.