Chapter 1: Understanding the Fibonacci Sequence

The Fibonacci sequence stands out as one of the most recognized and analyzed sequences globally. For those unfamiliar, this sequence is defined such that each term is the sum of the two preceding terms, represented mathematically as F_n = F_(n-1) + F_(n-2), starting with F_0 = 0 and F_1 = 1. In this article, we will explore how to calculate the sum of this sequence, revealing the underlying digits of the Fibonacci series.

Initially, let’s examine the recurrence relation:

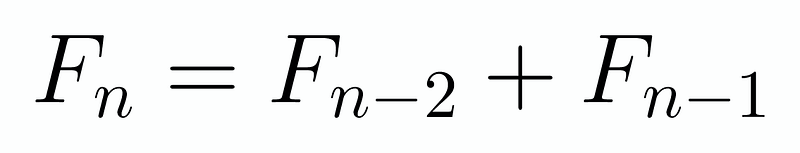
Could we derive a more straightforward expression for F_n? If we do so, it might also simplify the process of finding the sum. Let’s delve into this idea further. By rearranging, we achieve:

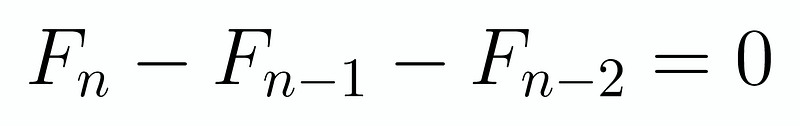
Readers should recognize that recurrence relations serve as discrete counterparts to differential equations, and the techniques to solve them are quite similar. Therefore, we will analyze the auxiliary equation to derive the general pattern:

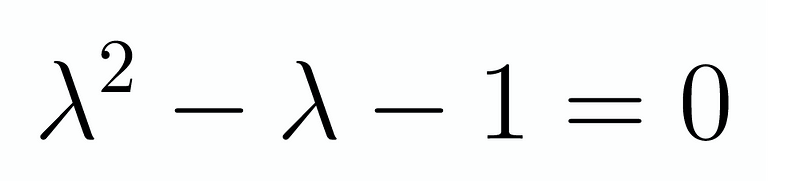
The solutions to this equation determine the behavior of F_n. Using the quadratic formula, we can derive the following results for ?:

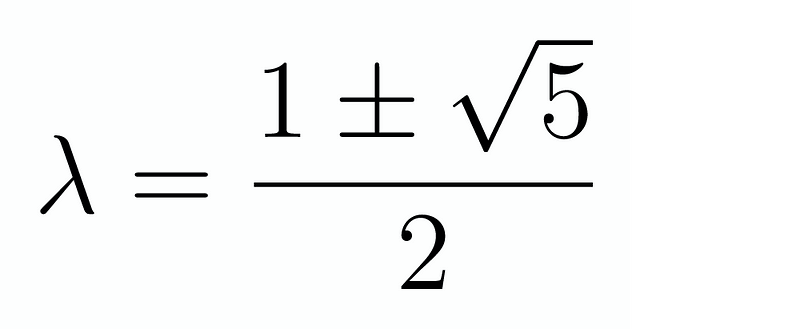
Thus, we can express F_n in the following manner, where A and B are constants to be determined:

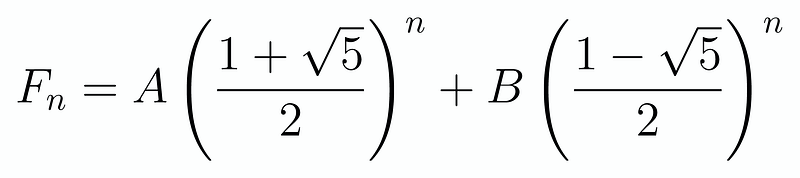
Since we know the values of F_0 and F_1, we can substitute these into the equation to form a set of simultaneous equations:

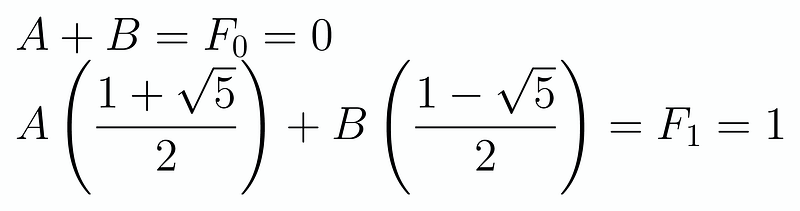
This process resembles solving any other simultaneous equations, albeit with less conventional coefficients. Although the solution process can be tedious, generally, we find A = 1/sqrt(5) and B = -1/sqrt(5). This formula, known as Binet's formula, has a unique connection to the golden ratio, though we won’t explore that further here.

Now, we can incorporate this into our series:

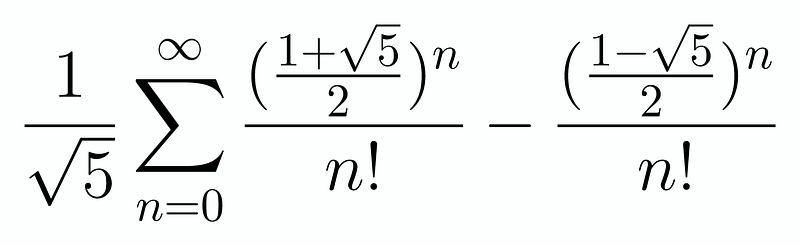
At first glance, this might not appear to be an improvement, but let’s recall the series representation for e^x, which converges universally:

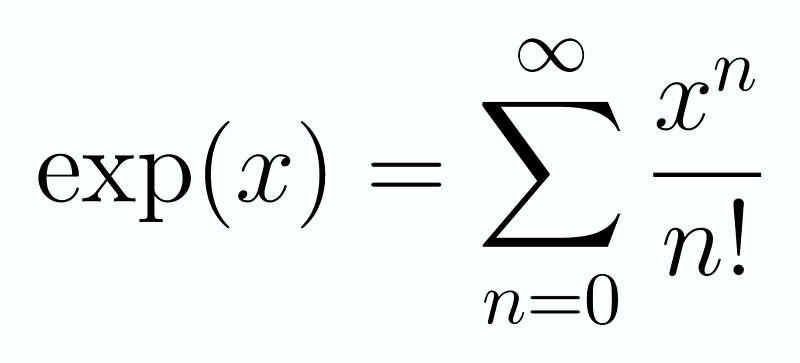
This is precisely the form we have! By substituting our values for x, we arrive at our final result:

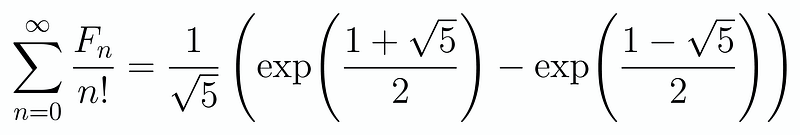
For those who prefer a concise version:

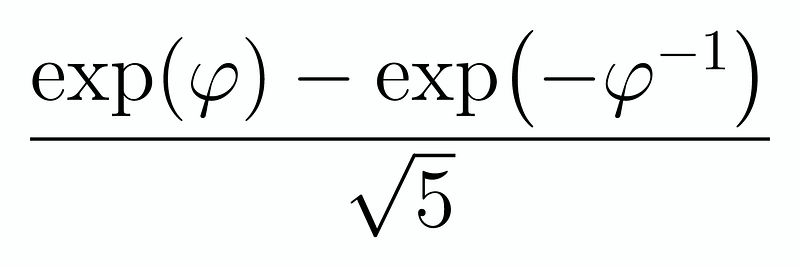
Where φ represents the golden ratio.

Chapter 2: Video Insights on Fibonacci Sums

In this video, titled "Sum of Fibonacci," viewers will uncover the intricacies behind calculating Fibonacci sums and their mathematical relevance.

The second video, "Sum of Fibonacci Numbers Trick," presents a clever method to simplify the calculation of Fibonacci sums, making it accessible to a wider audience.