Exploring the Strong Law of Small Numbers Through Humor
Written on
Chapter 1 Understanding the Strong Law of Small Numbers
The truth often resonates more when infused with humor!

Richard K. Guy authored a thought-provoking article on the strong law of small numbers in 1988. While much of mathematics focuses on exotic and vast numbers such as infinity or googol, Guy directed his attention toward the quirks and challenges of smaller numbers—those within a countable range.
With a playful tone, he suggested that the available small numbers are insufficient for the numerous demands placed upon them. He humorously articulated two critical observations:
- “Capricious coincidences cause careless conjectures.”
- “Initial irregularities inhibit incisive intuition.”
— R.K. Guy
If these statements seem perplexing at first, rest assured that clarity will emerge as we delve deeper. Guy aimed to illustrate how patterns can often be misleading when we work with small numbers. He provided various examples that indicated small numbers might appear to follow certain patterns that are, in reality, deceptive.
In this article, I will explore and illustrate some of Guy’s examples to enhance our understanding of the challenges we encounter with everyday numbers. These challenges frequently parallel real-life situations, where we mistakenly equate the frequency of an event with absolute truth.
Section 1.1 Perfect Squares and Their Deceptive Nature
Let’s begin by analyzing small numbers that are perfect squares: 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100, corresponding to the squares of integers 1 through 10.
This observation leads us to conclude that 10% of the first hundred numbers are perfect squares. Based on this premise, one might easily deduce that perfect squares make up about 10% of all numbers. But let’s put that assumption to the test.
If we expand our view to the first thousand numbers, we find that only about 3% are perfect squares. As we continue to extend the range, this percentage diminishes further. In fact, as we approach infinity, the proportion of perfect squares tends towards zero. Thus, anyone residing in an “Infinity-Land” might conclude that perfect squares are virtually nonexistent, presenting an inverse fallacy to our initial assumption.
Section 1.2 Investigating Fermat’s Prime Patterns
Consider the following inquiry regarding prime patterns:
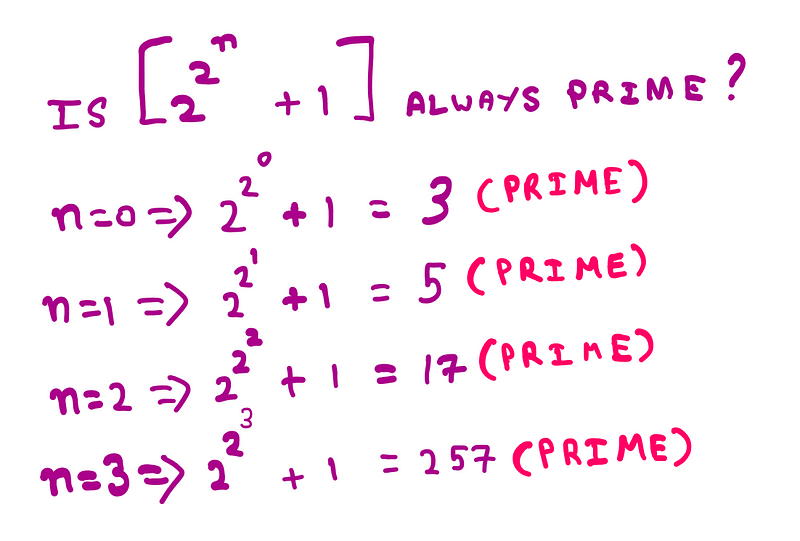
As we examine positive integers for ( n ), we initially yield prime results. However, this pattern shifts as we continue:
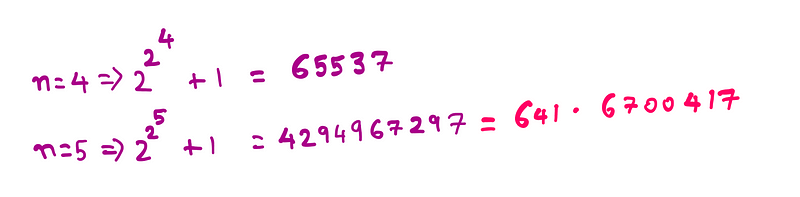
These results reveal a non-prime number, and the finiteness of this set remains unknown. These numbers, known as Fermat primes, are named after Pierre de Fermat, who proposed the initial claim, later disproven by Leonhard Euler.
Chapter 2 Patterns in Prime Numbers
Let’s examine another claim and the resulting pattern:
Are numbers of the form 3…31 always prime?
- 31 — Prime Number.
- 331 — Prime Number.
- 3331 — Prime Number.
- 33331 — Prime Number.
- 333331 — Prime Number.
This pattern appears compelling as we continue testing:
- 3333331 — Prime Number.
- 33333331 — Prime Number.
- 333333331 = 17 * 19607843 — Not Prime!
This example illustrates the deceptive nature of perceived patterns. It underscores the distinction between a lack of evidence for exceptions and the existence of evidence for non-exceptions.
Section 2.1 The Impact of Deleting Numbers
Let’s explore another intriguing series, where we omit every other number (even numbers) and analyze the partial sums.
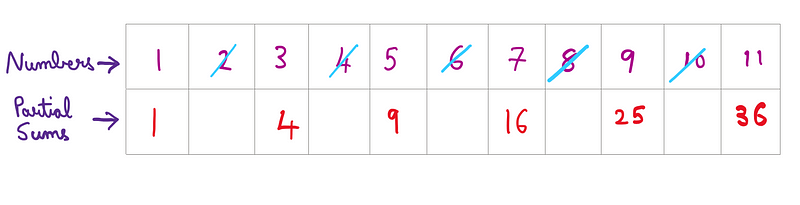
Initially, this series seems to suggest a trend towards perfect squares. Remarkably, this assertion holds true! This analysis process, known as Mössner’s theorem—originally merely a claim—was validated by Oskar Perron, further generalized by succeeding mathematicians.
What Does the Strong Law of Small Numbers Imply?
Guy’s humor was not just for amusement; his article conveyed a philosophical and statistical message, succinctly encapsulated by his own words:
“You can’t tell by looking.”
— R.K. Guy
Allow me to elaborate. Guy cautioned anyone working with small numbers to be wary of patterns that emerge. If you notice a pattern in a small sample size, resist the urge to draw conclusions hastily. The patterns observed might be misleading, and such hypotheses cannot be substantiated merely by visual inspection. This principle represents a contrast to the statistical law of large numbers.
While this may seem straightforward, Guy's brilliance lay in his ability to encapsulate this idea in counter-intuitive examples. Just when we believe we understand something, we become vulnerable to errors. His original article contains numerous other profound mathematical examples, which I will link in the references below.
Even experts can falter with small numbers; they can be elusive and deceptive. It's prudent to remain vigilant and validate your hypotheses before making assertions!
The first video, "Strong Law of Small Numbers - Numberphile - YouTube," illustrates how small number patterns can mislead our understanding of mathematics.
The second video, "What is...the strong law of small numbers? - YouTube," further explores the implications of this fascinating mathematical principle.
References: Richard K. Guy (scientific article), Alfred Mössner (scientific article — language: German), and Oskar Perron (scientific article — language: German).
I hope you found this exploration insightful and beneficial. If you appreciate my work, consider showing your support by clapping, following, and subscribing.
For further reading, you might enjoy “What Really Happens When You Measure A Coastline?” and “Are We Living In A Simulation?”
You can read the original essay here.